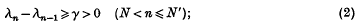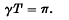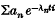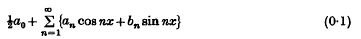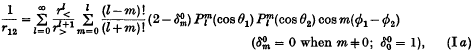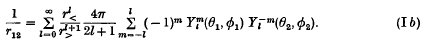Research Article
The distribution of the integers N for which {θN} < φ
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 525-534
-
- Article
- Export citation
A further note on trigonometrical inequalities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 535-537
-
- Article
- Export citation
Sets of uniqueness for trigonometric series and integrals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 538-548
-
- Article
- Export citation
The extremal values of Legendre polynomials and of certain related functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 549-554
-
- Article
- Export citation
Two maximal subgroups of a collineation group in five dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 555-569
-
- Article
- Export citation
A new method for the evaluation of zeros of Bessel functions and of other solutions of second-order differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 570-580
-
- Article
- Export citation
On the asymptotic probability distribution for certain Markoff processes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 581-594
-
- Article
- Export citation
Stochastic processes relating to particles distributed in a continuous infinity of states
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 595-602
-
- Article
- Export citation
Unsteady laminar flow of gas near an infinite flat plate
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 603-613
-
- Article
- Export citation
The characterization of quantum-mechanical operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 614-619
-
- Article
- Export citation
The paradox of separated systems in quantum theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 620-625
-
- Article
- Export citation
On the expansion of a Coulomb potential in spherical harmonics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 626-633
-
- Article
- Export citation
Conduction of heat in a solid with a power law of heat transfer at its surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 634-641
-
- Article
- Export citation
Research Notes
A theorem of Vinogradoff on uniform distribution
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 642-644
-
- Article
- Export citation
The boundary layer of a class of infinite yawed cylinders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 645-648
-
- Article
- Export citation
On the interaction of vector mesons with nucleons
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 649-650
-
- Article
- Export citation
A note on magnetic fields in conducting materials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 651-654
-
- Article
- Export citation
Proceedings
Proceedings at the Meetings Held During the Session 1949–1950: Annual General Meeting
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 655-658
-
- Article
- Export citation
Statement of Accounts
The Cambridge Philosophical Society Statement of Accounts for the Year Ending 31 July 1949
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 659-661
-
- Article
- Export citation
Front matter
PSP volume 46 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f6
-
- Article
-
- You have access
- Export citation