Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T08:33:31.579Z Has data issue: false hasContentIssue false
  • English
  • Français

On the expansion of a Coulomb potential in spherical harmonics

Published online by Cambridge University Press:  24 October 2008

B. C. Carlson  and
G. S. Rushbrooke
B. C. Carlson
Affiliation:
Clarendon LaboratoryOxford
G. S. Rushbrooke
Affiliation:
Clarendon LaboratoryOxford
Get access Rights & Permissions [Opens in a new window]

Extract

The addition theorem for Legendre functions leads, as is well known, to a useful expansion formula of importance in the theory of electrostatic potentials,

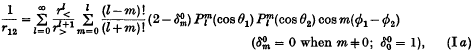
or, in an alternative notation,

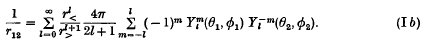
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 4 , October 1950 , pp. 626 - 633
Copyright
Copyright © Cambridge Philosophical Society 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Eyring, H., Walter, J. and Kimball, G. E., Quantum chemistry (New York, 1944), p. 371.Google Scholar

‡ Hobson, E. W., The theory of spherical and ellipsoidal harmonics (Cambridge, 1931), pp. 90, 99.Google Scholar

§ Our is the same for all m as defined by Condon, E. U. and Shortley, G. H., The theory of atomic spectra (Cambridge, 1935), p. 52.Google Scholar

† Terms up to an including R −6 are correctly given in Cartesian coordinates by Heller, R., J. Chem. Phys. 9 (1941), 156.CrossRefGoogle Scholar Elsewhere the quadrupole term has often been written with one or more errors of sign.

† Wigner, E., Gruppentheorie (Braunschweig, 1931), p. 206.Google Scholar Also Condon and Shortley, loc. cit. p. 75.

‡ Hobson, E. W., loc. cit. §§ 83, 85, 88, 101 and 103.

† Gatint, J. A., Philos. Trans. A, 228 (1929), 151.Google Scholar Gaunt's formula is written in notation very similar to ours by Condon and Shortley, loc. cit. p. 176. Our l 1, m 1, l 2, m 2, L are to be identified with their l, m, l′, m′, l″, and the integral on the left side of (16) is 1/√(2π) times the integral on the left side of their equation (11).