Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T20:14:41.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Sets of uniqueness for trigonometric series and integrals

Published online by Cambridge University Press:  24 October 2008

R. Henstock
R. Henstock
Affiliation:
Birkbuck CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Extract

It is well known that, if a trigonometric series

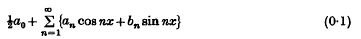
converges to zero in 0 ≤ x < 2π then all the coefficients are zero. To generalize this property of the series, sets of uniqueness have been defined. A point-set E in 0 ≤ x < 2π is a set of uniqueness if every series (0·1), converging to zero in [0, 2π) − E, has zero coefficients. Otherwise E is a set of multiplicity. For example, every enumerable set is a set of uniqueness. An account of the theory may be found in Zygmund (2), chapter 11, pp. 267 et seq.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 4 , October 1950 , pp. 538 - 548
Copyright
Copyright © Cambridge Philosophical Society 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Wolf, F.Contributions to a theory of summability of trigonometric integrals. (University of California Press, 1947.)Google Scholar
(2)Zygmund, A.Trigonometrical series. (Warsaw, 1935.)Google Scholar
(3)Zygmund, A.On trigonometric integrals. Ann. Math. 48 (1947), 393–440.Google Scholar
(4)Offord, A. C.Note on the uniqueness of the representation of a function by a trigonometric integral. J. London Math. Soc. 11 (1936), 171–174.CrossRefGoogle Scholar