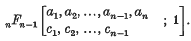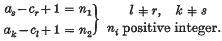Research Article
Some large classes of n-valued Sheffer functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-211
-
- Article
- Export citation
Common solutions to a pair of linear matrix equations A1XB1 = C1 and A2XB2 = C2
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-216
-
- Article
- Export citation
Zeeman's Catastrophe Machine
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 217-226
-
- Article
- Export citation
On Moore graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 227-236
-
- Article
- Export citation
The combinatorial structure of the Hughes–Zassenhaus plane of order 25
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 237-245
-
- Article
- Export citation
The (11, 3)-arcs of the Galois plane of order 5
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 247-250
-
- Article
- Export citation
Some generalizations of the Borsuk–Ulam theorem and applications to realizing homotopy classes by embedded spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-256
-
- Article
- Export citation
Convergence of measurable operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-268
-
- Article
- Export citation
Zeros of generalized hypergeometric functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 269-276
-
- Article
- Export citation
On operator equations and variational principles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-279
-
- Article
- Export citation
On the eigenvectors of the energy-momentum tensor in the Einstein–Maxwell theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-288
-
- Article
- Export citation
The asymptotic analysis of canonical problems in high-frequency scattering theory: I. Stratified media above a plane boundary
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 289-312
-
- Article
- Export citation
The asymptotic analysis of canonical problems in high-frequency scattering theory: II. The circular and parabolic cylinders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 313-332
-
- Article
- Export citation
On mass transport induced by interfacial oscillations at a single frequency
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 333-347
-
- Article
- Export citation
The reflexion of an acoustic pulse by a plane vortex sheet
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 349-364
-
- Article
- Export citation
The vorticity equation as an angular momentum equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-367
-
- Article
- Export citation
Axial radiation reception
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-395
-
- Article
- Export citation
Front matter
PSP volume 74 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 74 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation


 , of order 25 is the simplest of the exceptional Hughes planes (see, e.g. (1), p. 391).
, of order 25 is the simplest of the exceptional Hughes planes (see, e.g. (1), p. 391).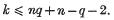
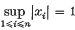 . Let
. Let 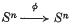 be a piecewise linear (
be a piecewise linear (