Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-20T03:56:54.036Z Has data issue: false hasContentIssue false
  • English
  • Français

The (11, 3)-arcs of the Galois plane of order 5

Published online by Cambridge University Press:  24 October 2008

D. L. Bramwell  and
B. J. Wilson
D. L. Bramwell
Affiliation:
Chelsea College, University of London
B. J. Wilson
Affiliation:
Chelsea College, University of London
Get access Rights & Permissions [Opens in a new window]

Extract

1. It was shown by Barlotti(1) that the number, k, of points on a (k, n)-arc in a Galois plane S2, q, of order q, where n and q are coprime, satisfies

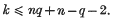
Regular arcs, in which all the points are of the same type have been studied by Basile and Brutti(2) and, for n = 3 by d'Orgeval(4). By means of an electronic computer Lunelli and Sce(5) have enumerated many arcs in Galois planes of low order. The object of this note is to show how the (11, 3)-arcs of S2, 5, none of which is regular, may be described using only geometrical properties.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 2 , September 1973 , pp. 247 - 250
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)BarLotti, A.Sui (k, n)-archi di un piano lineare finito. Boll. Un. Mat. Ital. (3), 11 (1956), 553–6.Google Scholar
(2)Basile, A. and Brutti, P.On the completeness of regular (q(n − i) + m; n)-arcs in a finite projective plane. Geometriae Dedicata 1 (1972).Google Scholar
(3)Bramwell, D. Ph.D. thesis: University of London, 1973.Google Scholar
(4)D'Orgeval, B.Sur certains (k, 3)-arcs in Geometrie de Galois. Bull. Acad. Roy. Belg. XLVI, (1960), 597–603.Google Scholar
(5)Lunelli, L. and Sce, M.Considerazioni arithmetiche e risultati sperimentali sui (K; n)q-archi. Lombardo Accord. Sci. Lett. Rendic 98 (1964), 3–52.Google Scholar
(6)Segre, B.Lectures on Modern Geometry. Edizioni Cremonese (Roma, 1961).Google Scholar
(7)Segre, B.Introduction to Galois Geometries. Mem. Accord. Naz. Lincei (8), 8 (1967), 137–236.Google Scholar
(8)Wilson, B. Ph.D. thesis: University of London, 1970.Google Scholar