In a Newtonian fluid, in which the body forces are conservative, in which the pressure is a function only of density and in which the kinematic viscosity v is uniform, the vorticity ω satisfies the equation

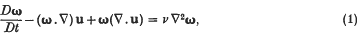
where u is the velocity field, so that ω = ▿ × u. This equation is normally derived by taking the curl of the Navier–Stokes equations. However, the vorticity has many interpretations in terms of the angular velocity of elements of fluid and it is natural to expect that (1) can be derived by equating the rate of change of the angular momentum of a small material volume element about its centre of mass with the moment of the forces acting on the element. Such a derivation is presented here in the hope that it may be of pedagogic interest.