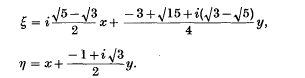Let Z, Q, C denote respectively the ring of rational integers, the field of rational numbers and the field of complex numbers. Minkowski (4) solved the problem of minimizing
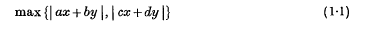
for x, y ∈ Z(i) or Z(ρ), where a, b, c, d ∈ C have fixed determinant Δ ≠ 0. Here ρ = exp 2/3πi, and Z(i) and Z(p) are the rings of integers in Q(i) and Q(ρ) respectively. In fact he found the best possible results
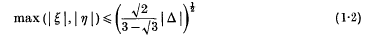
for Z(i), and

for Z(ρ), where
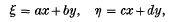
while Buchner (1) used Minkowski's method to show that
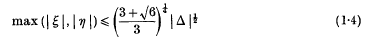
for Z(i√2). Hlawka(3) has also proved (1·2), and Cassels, Ledermann and Mahler (2) have proved both (1·2) and (1·3). In a paper being prepared jointly by H. P. F. Swinnerton-Dyer and the author, general problems of the geometry of numbers in complex space are discussed and a systematic method given for solving the above problem for all complex quadratic fields Q(ϑ). Here, ϑ is a non-real number satisfying. an irreduc7ible quadratic equation with rational coefficients. The above problem is solved in detail for Q(i√5), for which
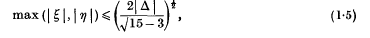
and the ‘critical forms’ can be reduced to