Let

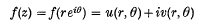
be a function regular for | z | < 1. With the hypotheses f(0) = 0 and

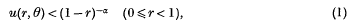
for some positive constant α, Cartwright(1) has deduced upper bounds for |f(z) | in the unit circle. Three cases have arisen and according as (1) holds with α < 1, α = 1 or α > 1, the bounds on each circle | z | = r are given respectively by

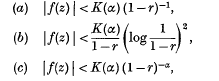
K(α) being a constant which depends only on the corresponding value of α which occurs in (1). We shall always use the symbols K and A to represent constants dependent on certain parameters such as α, not necessarily having the same value at each occurrence.