From the fact that Hausdorff s-dimensional measure is a regular Carathéodory outer measure follows (see Saks (3), ch. II, §§ 6, 8) the standard result: Theorem A. If {En} is any increasing sequence of sets, then ∧sEn → ∧s(ΣEn) as n → ∞.

Since ∧s X is denned (for every set X) as 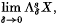, the problem arises whether for every positive δ and every increasing sequence of sets one can prove

Now there are four possible ways of defining 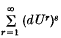; it is the lower bound of 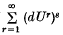taken over coverings ΣUr of X by convex sets, but in most applications it is not important whether the restriction on the convex sets is that they shall be (i) open and of diameter less than δ, (ii) closed and of diameter less than δ, (iii) open and of diameter not exceeding δ, or (iv) closed and of diameter not exceeding δ.