Article contents
The transmission of surface waves under surface obstacles
Published online by Cambridge University Press: 24 October 2008
Abstract
A train of surface waves (water waves under gravity) is normally incident on a cylinder with horizontal generators fixed near the free surface, and is partially transmitted and partially reflected. At a great distance behind the cylinder the wave motion tends to a regular wave train travelling towards infinity; the ratio of its amplitude to the amplitude of the incident wave is the transmission coefficient 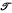 . The transmission coefficient is studied when the wavelength is short compared to the dimensions of the body; physically (though not for engineering applications) this is the most interesting range of wavelengths, which corresponds to the range of shadow formation and ray propagation in optics and acoustics. The waves are then confined to a thin layer near the free surface, and the transmission under a partially immersed obstacle is then small. In the calculation the boundary condition at the free surface is linearized, viscosity is neglected, and the motion is assumed to be irrotational.
. The transmission coefficient is studied when the wavelength is short compared to the dimensions of the body; physically (though not for engineering applications) this is the most interesting range of wavelengths, which corresponds to the range of shadow formation and ray propagation in optics and acoustics. The waves are then confined to a thin layer near the free surface, and the transmission under a partially immersed obstacle is then small. In the calculation the boundary condition at the free surface is linearized, viscosity is neglected, and the motion is assumed to be irrotational.
At present the transmission coefficient is known only for a few configurations, all of them relating to infinitely thin plane barriers. A method is now given which is applicable to cylinders of finite cross-section and which is worked out in detail for a half-immersed cylinder of circular cross-section. The solution of the problem is made to depend on the solution of an integral equation which is solved by iteration. Only the first two terms can be obtained with any accuracy, and it appears at first that this is not sufficient to give the leading term in the transmission coefficient at short wavelengths; this difficulty is characteristic of transmission problems. By various mathematical devices which throw light on the mechanism of wave transmission, it is, nevertheless, found possible to prove that the transmission coefficient for waves of short wavelength λ and period 2π/ω incident on a half-immersed circular cylinder of radius a is asymptotically given by
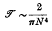
when N = 2πα/λ = ω2α/g is large. Earlier evidence had pointed towards an exponential law. It is suggested that transmission coefficients of order N−4 are typical for obstacles having vertical tangents and finite non-zero radius of curvature at the points where they meet the horizontal mean free surface. For obstacles having both front and rear face plane vertical to a depth a, 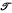 is probably of order e−2N approximately; if only one of the two faces is plane vertical,
is probably of order e−2N approximately; if only one of the two faces is plane vertical, 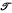 is probably of order e−N approximately. Thus
is probably of order e−N approximately. Thus 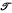 is seen to depend critically on the details of the cross-section.
is seen to depend critically on the details of the cross-section.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 3 , July 1961 , pp. 638 - 668
- Copyright
- Copyright © Cambridge Philosophical Society 1961
References
REFERENCES
- 28
- Cited by


