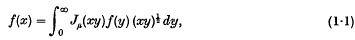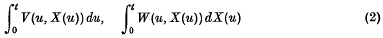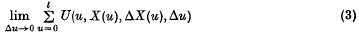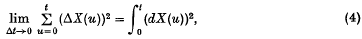Research Article
Testing the independence of a system of axioms, using a logical computer
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 443-448
-
- Article
- Export citation
Waring's problem in algebraic number fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 449-459
-
- Article
- Export citation
Tensor operators under semi-simple groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 460-468
-
- Article
- Export citation
Representations of the n-dimensional rotation group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-475
-
- Article
- Export citation
Construction of orders in Abelian groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 476-482
-
- Article
- Export citation
Simple reduction theorems for extension and torsion functors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-488
-
- Article
- Export citation
Natural maps of extension functors and a theorem of R. G. Swan
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-502
-
- Article
- Export citation
The real solutions of a certain non-linear system of equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 503-506
-
- Article
- Export citation
On manifolds containing a submanifold whose complement is contractible
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 507-515
-
- Article
- Export citation
The number of polygons on a lattice
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 516-523
-
- Article
- Export citation
On the connexion between Hausdorff measures and generalized capacity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 524-531
-
- Article
- Export citation
Eigenvalues and eigenfunctions of finite-difference operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 532-546
-
- Article
- Export citation
An infinite Legendre integral transform and its inverse
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 547-560
-
- Article
- Export citation
Self reciprocal properties of certain functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 561-567
-
- Article
- Export citation
Equations for stochastic path integrals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 568-573
-
- Article
- Export citation
A mathematical problem in population genetics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 574-582
-
- Article
- Export citation
A central limit theorem for systems of regressions*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 583-588
-
- Article
- Export citation
The physical interpretation of entity-structure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 589-605
-
- Article
- Export citation
Transport properties of thin metallic films
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 606-622
-
- Article
- Export citation
Note on an electrified circular disk situated inside an earthed coaxial infinite hollow cylinder
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 623-627
-
- Article
- Export citation

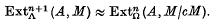
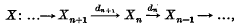
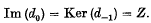
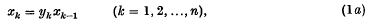
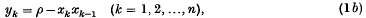
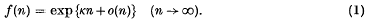
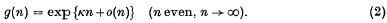
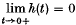 , Hausdorff (10) in 1918 denned a Carathéodory measure with respect to
, Hausdorff (10) in 1918 denned a Carathéodory measure with respect to 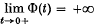 , Frostman(9) in 1935 denned capacity with respect to Φ(
, Frostman(9) in 1935 denned capacity with respect to Φ(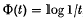 , Φ(
, Φ(