Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-02T03:33:16.835Z Has data issue: false hasContentIssue false
  • English
  • Français

Some self-reciprocal functions and kernels

Published online by Cambridge University Press:  24 October 2008

V. Lakshmikanth
V. Lakshmikanth
Affiliation:
Osmania UniversityHyderabad (A.P.), India
Get access Rights & Permissions [Opens in a new window]

Extract

The aim of this note is to find out some self-reciprocal functions and kernels for Fourier-Bessel integral transforms. Following Hardy and Titchmarsh(i), we shall denote by Rp the class of functions which satisfy the homogeneous integral equation

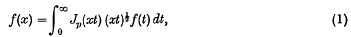
where Jp(x) is a Bessel function of order p ≥ − ½. For particular values of p = ½, − ½, we write Rs and Rc irrespectively.

Type
Research Notes
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 3 , July 1961 , pp. 690 - 692
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hardy, G. H. and Titchmarsh, E. C.Self reciprocal functions. Quart. J. Math. (2), 1 (1930), 196–231.CrossRefGoogle Scholar
(2)Lakshmikanth, V.Some self-reciprocal functions. Proc. Nat. Acad. Sci. India, Part A, 28 (1959), 246–8.Google Scholar
(3)Lakshmikanth, V. On the relation between the self-reciprocal functions and kernels (submitted for publication).Google Scholar
(4)Rao, M. E. NarayanSome general kernels for the derivation of self reciprocal functions. Proc. Indian Acad. Sci. Sect. A, 50 (1959), 385–91.CrossRefGoogle Scholar
(5)Gupta, H. C.TWO theorems on self-reciprocal functions. J. Indian Math. Soc. N.S. 9 (1945), 66–8.Google Scholar
(6)Watson, G. N.Theory of Bessel functions (Cambridge, 1922).Google Scholar