Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T05:23:18.074Z Has data issue: false hasContentIssue false
  • English
  • Français

Equations for stochastic path integrals

Published online by Cambridge University Press:  24 October 2008

M. S. Bartlett
M. S. Bartlett
Affiliation:
University CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Extract

Apart from the study of the integral

where {X(u)} is a stationary Gaussian process with autocorrelation function ρ(t), by Kac and Siegert(1), most stochastic functionals of the general type

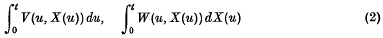
have been considered for {X(u)} either additive or Markovian (see, for example, (2), (3)), and in the Markovian case only for diffusion-type processes (Darling and Siegert (4)). More general approaches exist (e.g. (5), (6)), but seem less concerned with the investigation of specific problems. Some preliminary remarks here are therefore aimed at examining the structure of integrals of type (2), or such further extensions of the formal Riemann sum type

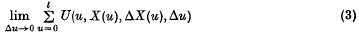
that would be expected to have well-behaved distributional properties for {X(t)} Markovian, and associated equations for studying these properties. As an example, the sum

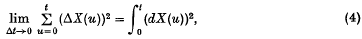
say, is considered (i) for the normal linear Markovian process, (ii) for simple birth-and-death and emigration—immigration processes.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 3 , July 1961 , pp. 568 - 573
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kac, M. and Siegert, A. J. F.On the theory of random noise in radio receivers with square law detectors. J. Appl. Phys. 18 (1947), 383.Google Scholar
(2)Kac, M.Probability and related topics in physical sciences (New York, 1959).Google Scholar
(3)Kozin, F.On the quadratic detector—I. J. Math. Phys. 38 (1959), 119.CrossRefGoogle Scholar
(4)Darling, D. A. and Siegert, A. J. F.On the distribution of certain functionals of Markoff processes. Rand Corporation Report (1953).Google Scholar
(5)Cameron, R. H. and Donsker, M. D.Inversion formuale for characteristic functionals of stochastic processes. Ann. Math. Princeton, 69 (1959), 15.CrossRefGoogle Scholar
(6)Dynkin, E. B.Transformations of Markovian processes connected with additive functionals. 4th Symposium on Math. Stat. and Probability, Berkeley (1960) (to be published).Google Scholar
(7)Bartlett, M. S.An introduction to stochastic processes (Cambridge, 1955).Google Scholar
(8)Bartlett, M. S.A remark on stochastic path integrals. Nature, Lond., 187 (1960), 968.Google Scholar
(9)Waugh, W. A. O'N.Conditioned Markov processes. Biometrika, 45 (1958), 241.Google Scholar
(10)Discussion at the Symposium on Stochastic processes. J. Roy. Statist. Soc. Ser. B, 11 (1949), 150.Google Scholar
(11)Kendall, D. G.On the generalized ‘birth-and-death’ process. Ann. Math. Statist. 19 (1948), 1.Google Scholar