Research Article
Bounded and invariant elements in 2-firs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-12
-
- Article
- Export citation
Groups with every proper quotient finite
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-391
-
- Article
- Export citation
A note on residually finite groups†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 255-256
-
- Article
- Export citation
On subgroups of amalgamated free products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-23
-
- Article
- Export citation
A note on the homotopy type of PL2
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-258
-
- Article
- Export citation
A synthetic proof of de Longchamps' chain
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-400
-
- Article
- Export citation
Massey products in K-theory. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 259-289
-
- Article
- Export citation
A second anticommutant theorem for symmetric ternary algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-52
-
- Article
- Export citation
Matchings in Arbitrary Graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-407
-
- Article
- Export citation
Factorizations of completely positive matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 53-58
-
- Article
- Export citation
On scalar-type spectral operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 409-410
-
- Article
- Export citation
On the homotopy-symmetry of sphere bundles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-294
-
- Article
- Export citation
On the differential topology of space-time†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 295-296
-
- Article
- Export citation
The power inequality on Banach spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 411-415
-
- Article
- Export citation
Homology, Hilbert functions, and the conservation of number
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 59-70
-
- Article
- Export citation
Some remarks on the Kakeya problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-421
-
- Article
- Export citation
Summability methods which include the Riesz typical means. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-300
-
- Article
- Export citation
Collapsing K × I to vertical segments
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-74
-
- Article
- Export citation
An extension of Lukacs's result
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-303
-
- Article
- Export citation
General relativity from gauge invariance
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 423-442
-
- Article
- Export citation

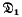 for the class of groups all of whose non-trivial normal subgroups have finite index. Thus, rather obviously, finite groups, simple groups, and the infinite cyclic and dihedral groups all lie in the class
for the class of groups all of whose non-trivial normal subgroups have finite index. Thus, rather obviously, finite groups, simple groups, and the infinite cyclic and dihedral groups all lie in the class 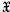 -group, all of whose proper quotients are finite
-group, all of whose proper quotients are finite 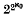
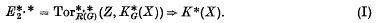
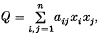 with
with