No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
1. Introduction. Flow of viscous fluid at low Reynolds number has attracted a great deal of attention over the last hundred years or so and is still an area of active research at the present time. For a general background on this field, we refer the reader to Langois(4). The present paper is concerned with steady flow past a finite flat plate which spans a long rectangular channel, of large aspect-ratio, at the centre ‘line’ (see Fig. 1). The flow is motivated by a constant pressure difference which is applied
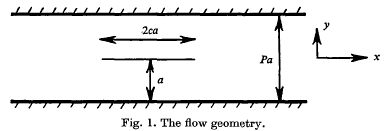
between the ends of the channel. We examine such flows when the Reynolds number based on the semi-channel height, a, is much less than 1. Our main task is to show that Stokes approximation, i.e. neglection of the inertia terms, is uniformly valid † over the whole flow field. (†Such a result contrasts with the non-uniformity of the approximation when the channel walls are removed and the external flow is a uniform stream.) Harper & Chang (1) who treat the corresponding problem for a circular cylinder, give a full account of recent theoretical and experimental work on this class of fluid flows. We shall therefore defer comments on related papers until the appropriate part of the text.