No CrossRef data available.
The spectrum of the self-adjoint partial differential equation in any domain
Published online by Cambridge University Press: 24 October 2008
Extract
The object of this paper is to obtain the general solution to the self-adjoint partial differential equation in n dimensions

where pij, q and ρ and bounded, continuous functions of (x1,…, xn) in a domain D and on its boundary, and where ∑pijXiXj≥0 for all (x1,…, xn) of D and all X1,…, Xn. The domain D is an n-dimensional domain and may be either the whole or part of a Riemann surface space of n dimensions. Its boundary is to consist of any number, zero, finite or enumerable, of continuous continua of n − 1 dimensions. These terms will be explained in paragraph II. The solution u = u(x1,…, xn; t) will be valid for (x1,…, xn) in D and t ≥ 0, and will satisfy boundary conditions of the type 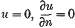 or similar, these conditions becoming identical at any part of the boundary of D that lies at infinity.
or similar, these conditions becoming identical at any part of the boundary of D that lies at infinity.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 1 , January 1933 , pp. 23 - 44
- Copyright
- Copyright © Cambridge Philosophical Society 1933
References
* Hellinger, E., Journ. f. Math. 136 (1909), 210–271Google Scholar; Hahn, H., Monats. Math. Phys. 23 (1912), 161–224CrossRefGoogle Scholar; Hyslop, J., Proc. London Math. Soc. (2), 24 (1926), 264–304.CrossRefGoogle Scholar
* Carathéodory, , Math. Ann. 73 (1913), 323–370.CrossRefGoogle Scholar
* The conditions of continuity as used in a former paper are not bounded (Steen, , Proc. Camb. Phil. Soc. 28 (1932), 31–32)CrossRefGoogle Scholar, they should therefore be altered to the above form.
* See Steen, , Proc. Camb. Phil. Soc. 28 (1932), 27–29.CrossRefGoogle Scholar
* I am indebted to Mr Cornock of the General Electric Company for bringing to my notice systems of equations.


