Nöther in his classical paper Zur Theorie des eindeutigen Ent-sprechens algebraischer Gebilde has given a set of sixteen examples of the computation of his invariants pn, p(2), p(1) for algebraic surfaces in ordinary space. In the following I discuss, as a matter of some interest, the birational transformation of his surfaces into surfaces which are non-singular.

1. In a recent paper in these Proceedings by Mr H. Lob, and iu an earlier paper by Mr F. P. White, it has been shown how the well-known chains of theorems in plane geometry discovered by Morley and Clifford may be proved by projection from higher space. A curve of order n in space of n dimensions and certain derived loci are projected from one, or two, or three, …, or n − 2, out of n + 1 chosen points of the curve upon a plane which contains two further points of the curve. The n + 1 lines of the plane which form the starting-point of each chain of results as originally proved (and which are obtained in various ways in the course of the projections) are actually the lines in which the plane of projection is met by the primes containing n out of the n + 1 points. Now, with the standard equations of such a curve in [n], viz.

The purpose of this paper is to provide a point of vantage from which to attack combinatorial problems in what may be termed modern, synthetic, or abstract algebra. In this spirit, a research has been made into the consequences and applications of seven or eight axioms, only one [V] of which is itself new.

This third and last part of the paper is concerned with the interpretation of the Schläfli symbol {k1, k2, …, km−1} when the k's are unrestricted. It is shown that, whenever the k's are integers (greater than 2), the symbol represents a polytope in a generalized space having time-like as well as space-like dimensions.

1. As long ago as 1878 Neumann gave a formula expressing the product of two Legendre polynomials as a sum of such polynomials. In the same year Adams gave an inductive proof, and obtained the result in the form

The object of this paper is to obtain the general solution to the self-adjoint partial differential equation in n dimensions

where pij, q and ρ and bounded, continuous functions of (x1,…, xn) in a domain D and on its boundary, and where ∑pijXiXj≥0 for all (x1,…, xn) of D and all X1,…, Xn. The domain D is an n-dimensional domain and may be either the whole or part of a Riemann surface space of n dimensions. Its boundary is to consist of any number, zero, finite or enumerable, of continuous continua of n − 1 dimensions. These terms will be explained in paragraph II. The solution u = u(x1,…, xn; t) will be valid for (x1,…, xn) in D and t ≥ 0, and will satisfy boundary conditions of the type or similar, these conditions becoming identical at any part of the boundary of D that lies at infinity.

1. In a recent paper I established new conditions for a form φ of order n, homogeneous in r + 1 variables, to be expressible as the sum of nth powers of linear forms in these variables; and for this expression, if it exists, to be unique. These conditions, I further showed, may be stated as general theorems regarding the secant spaces of manifolds Mr in higher space, namely:

Necessary and sufficient conditions that through a general point of a space N, of h (r + 1) − 1 dimensions, there passes (i) no, (ii) a unique (h − 1)-dimensional space containing h points of a manifold Mr lying in N are that

(i) the space projecting a general point of Mr from the join of h − 1 general r-dimensional tangent spaces of Mr meets Mr in a curve, so that Mr cannot be so projected upon a linear space of r dimensions;

(ii) the space projecting a general point of Mr from the join of h − 1 general r-dimensional tangent spaces of Mr does not meet Mr again, so that Mr can be so projected, birationally, upon a linear space of r dimensions..

The algebraical foundation of this representation is very simple: it depends on the theorem

If a coordinate system in [m] is given, then in a general [k] of the [m] a unique set of k + 1 points can be found whose coordinates form the scheme

where h = m − k − 1, and n = (m − k)(k + 1) = kh + m.

In the following pages I have developed the theory of matrices by resolving them into parallel components arranged diagonally, rather than into the usual rows and columns. This treatment is natural in view of the fundamental fact that the resolution is undestroyed when matrices are formed into products (Theorem 2). It is closely related to the theory of continuants and of continued fractions. Certain features stand out in such a presentation—the distinction between the length and range of a diagonal (§ 4), that between regular and irregular diagonals (§ 6), and the use of equable partition (§ 7). The exact conditions for the existence of an rth root of a given singular matrix are examined in § 9 and summarized under the title, the condition of equability.

1. In a paper read to this Society Mr F. P. White has derived a remarkable chain of theorems in [n] which, for n = 2, becomes Clifford's chain. White's method is so elegant that, as he has restricted himself to curves going through two given points, it may be permissible to shew that his line of argument applies equally to curves going through three or more given points, thus producing other chains of theorems analogous to Clifford's. For this purpose it is necessary to consider the successive projections, not of a simplex, but of a figure of n, n − 1, n − 2,…vertices in [n].

The problem of discriminating between the different real forms of the rational twisted quartic was first attempted by Adler in 1882. His catalogue is incomplete and some of his results are inaccurate, as has been pointed out by Richmond †. The work was however superseded by a paper in 1891 by Rohn‡ who considered the curve in relation to its allied Steiner quartic surface; his results may be compared with those given in the final section of this paper. Substantially the same results were obtained by Vietoris§ who mapped the curve on a conic by a somewhat different method from that used by Adler.

1. A general threefold in [5] has an apparent double surface whose projection on to a [4] is a surface which contains a triple curve and which is characterised by the fact that it has no improper nodes; such surfaces have been considered in a previous paper. In the present note we consider a class of surfaces in [5] which possess triple curves and project into surfaces in [4] having improper nodes: these are the surfaces which represent the chords of a general curve of ordinary space upon a quadric primal Ω of [5]. For the representation of a line congruence of [3] by the points of a surface on Ω, reference may be made to a previous note, the results of which are used in the present work.

The investigations which follow were originally suggested by the now classical problem of Cayley, the determination of the condition that seven lines in space, of which no two intersect, should lie on a quartic surface. This problem suggests the consideration of the linear system of quartic surfaces which pass through six given lines, and this, essentially, is the basis of all that follows.

1. The surface here discussed arises most naturally in the study of a certain cubic primal in space of five dimensions. Let G be a cubic primal in five-dimensional space, containing two planes M1, M2 which do not intersect. From any point of G can be drawn one transversal to M1, M2; this does not meet G again, and meets a fixed prime p in one point. Thus G can be birationally projected upon p, and is rational.

The theory of the exact difference equation in the general linear case has been fully developed, but the corresponding theory for the non-linear equation of the first order does not appear to have been considered. In this paper necessary and sufficient conditions for the difference equation of the first order to be exact and the form of the primitive are obtained. It appears that two conditions are required for a difference equation to be exact, one of which is identically satisfied in the limiting case of the exact differential equation. These conditions are applied to determining the primitive in some cases where the conditions for exactness are not satisfied.

1. The classification of surfaces whose sections are hyperelliptic has been given by Castelnuovo and that of surfaces with sectional genus π = 3 by Castelnuovo† and Scorza. For higher values of π the work is naturally more complicated and the possible types far more numerous, but the problem is simplified if we restrict ourselves to the investigation of surfaces without singularities, generally lying in space Sr (r > 3). In the present paper we obtain all such surfaces having sectional genus four.

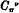The bisecant curves of a ruled surface, that is to say the curves on the surface which meet each generator in two points, are fundamental in the consideration of the normal space of the ruled surface. It is well known that if is a bisecant curve of order ν and genus π on a ruled surface of order N and genus P, then

provided that the curve has no double points which count twice as intersections of a generator of the ruled surface.

1·1. The points, tangents, osculating planes, …, osculating primes of a curve may be said to form a system which is characterised by the number of these elements which are incident with a prime, …, line, point, respectively. For the normal rational quartic curve the system is (4, 6, 6, 4); projection of this system from a general point gives the system (4, 6, 6) in [3]; section by a general prime gives the system (6, 6, 4). These two systems in [3], which are the systems with which we are concerned in this paper, are duals of one another, and will be called systems of the first and second kinds respectively.

1. In this note we investigate, from a new point of view, some properties of cubic primals in [4]. These are enunciated by Fano as follows.

1. In this paper I discuss the expression of the general form F of order n, homogeneous in r + 1 variables z0, z1,…, zl,…, zr, as the sum of the nth powers of h + H linear forms in these variables. I take h (> 0) of these linear forms to be undetermined, namely the forms

whose coefficients are undetermined; and I take the remaining H(≥0) linear forms to be assigned, namely the forms

whose coefficients are assigned.