Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T07:51:20.002Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple reduction theorems for extension and torsion functors

Published online by Cambridge University Press:  24 October 2008

D. G. Northcott
D. G. Northcott
Affiliation:
The UniversitySheffield
Get access Rights & Permissions [Opens in a new window]

Extract

Let Λ be a commutative ring with an identity element and c an element of Λ which is not a zero divisor Denote by Ω the residue class ring Λ/Λc. If now M is a Λ-module for which c is not a zero divisor, and A is an Ω-module, then a theorem of Rees (2) asserts that, for every non-negative integer n, we have a Λ-isomorphism

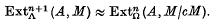
This reduction theorem has found a number of useful and interesting applications.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 3 , July 1961 , pp. 483 - 488
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cartan, H. and Eilenberg, S.Homological algebra (Princeton 1956).Google Scholar
(2)Rees, D.A theorem of homological algebra. Proc. Camb. Phil. Soc. 52 (1956), 605–10.CrossRefGoogle Scholar