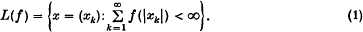Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maddox, I. J.
1987.
Inclusions between FK spaces and Kuttner's theorem.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 3,
p.
523.
Maddox, I. J.
1988.
Statistical convergence in a locally convex space.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 104,
Issue. 1,
p.
141.
Choudhary, B.
and
Parashar, S. D.
2002.
A sequence space defined by Orlicz functions.
Analysis in Theory and Applications,
Vol. 18,
Issue. 4,
p.
63.
Et, Mikail
2003.
Strongly almost summable difference sequences of order m defined by a modulus.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 40,
Issue. 4,
p.
463.
Bilgin, Tunay
2004.
Lacunary strong A-convergence with respect to a sequence of modulus functions.
Applied Mathematics and Computation,
Vol. 151,
Issue. 3,
p.
595.
Altin, Yavuz
Et, Mikâil
and
Tripathy, Binod Chandra
2004.
The sequence space on seminormed spaces.
Applied Mathematics and Computation,
Vol. 154,
Issue. 2,
p.
423.
Güngör, Mehmet
Et, Mikâil
and
Altin, Yavuz
2004.
Strongly (Vσ,λ,q)-summable sequences defined by Orlicz functions.
Applied Mathematics and Computation,
Vol. 157,
Issue. 2,
p.
561.
Karakaya, Vatan
and
Şimşek, Necip
2004.
On lacunary invariant sequence spaces defined by a sequence of modulus functions.
Applied Mathematics and Computation,
Vol. 156,
Issue. 3,
p.
597.
Et, M.
Gökhan, A.
and
Altinok, H.
2006.
On statistical convergence of vector-valued sequences associated with multiplier sequences.
Ukrainian Mathematical Journal,
Vol. 58,
Issue. 1,
p.
139.
Subramanian, N.
Nallaswamy, R.
and
Saivaraju, N.
2007.
Characterization of Entire Sequences via Double Orlicz Space.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2007,
Issue. ,
p.
1.
Savaş, Ekrem
2007.
On some new double sequence spaces defined by a modulus.
Applied Mathematics and Computation,
Vol. 187,
Issue. 1,
p.
417.
Kolk, Enno
and
Raidjõe, Annemai
2007.
The continuity of superposition operators on some sequence spaces defined by moduli.
Czechoslovak Mathematical Journal,
Vol. 57,
Issue. 3,
p.
777.
Shaw, Sen-Yen
and
Lin, Su-Hui
2007.
Strong and absolute almost-convergence of vector functions and related Tauberian theorems.
Journal of Mathematical Analysis and Applications,
Vol. 334,
Issue. 2,
p.
1073.
Savaş, Ekrem
2008.
(Aσ)-double sequence spaces defined by Orlicz function and double statistical convergence.
Computers & Mathematics with Applications,
Vol. 55,
Issue. 6,
p.
1293.
Bhardwaj, Vinod K.
and
Bala, Indu
2008.
Strong invariant A-summability with respect to a sequence of modulus functions in a seminormed space.
Demonstratio Mathematica,
Vol. 41,
Issue. 4,
Başarir, Metin
and
Altundağ, Selma
2008.
Some difference sequence spaces defined by a sequence of ϕ -functions.
Rendiconti del Circolo Matematico di Palermo,
Vol. 57,
Issue. 1,
p.
149.
Tripathy, Binod
Altin, Yavuz
and
Et, Mikail
2008.
Generalized difference sequence spaces on seminormed space defined by Orlicz functions.
Mathematica Slovaca,
Vol. 58,
Issue. 3,
p.
315.
Cheng, LiXin
Lin, GuoChen
Lan, YongYi
and
Liu, Hui
2008.
Measure theory of statistical convergence.
Science in China Series A: Mathematics,
Vol. 51,
Issue. 12,
p.
2285.
Başarir, Metin
and
Altundağ, Selma
2009.
On Generalized Paranormed Statistically Convergent Sequence Spaces Defined by Orlicz Function.
Journal of Inequalities and Applications,
Vol. 2009,
Issue. 1,
p.
729045.
Altin, Yavuz
2009.
Properties of some sets of sequences defined by a modulus function.
Acta Mathematica Scientia,
Vol. 29,
Issue. 2,
p.
427.