No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
In order to complete fully the proof of the fixed momentum-transfer dispersion relations for elastic scattering in quantum field theory given by Bremermann, Oehme and Taylor (1) it is necessary (2) to discuss more fully the analyticity of the absorptive part A(t, γ, Δ) in the mass variable γ. We are using the notation of (1), with 2Δ the momentum transfer and 4t2 the total energy of the initial system. For simplicity of discussion we will only treat the case of the elastic scattering of equal mass particles of mass m, the other cases discussed in (1) can be treated similarly. The crucial point of the proof, as first pointed out in (3), is to prove that
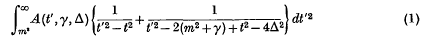
is regular in γ in a strip 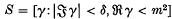 . It was only proved explicitly in (1) that A(t, γ, Δ) is regular for each t, in a strip
. It was only proved explicitly in (1) that A(t, γ, Δ) is regular for each t, in a strip 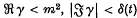 , where δ may depend on t. In order to prove the analyticity in S of the integral in equation (1) it is necessary to show that δ(t) may be chosen to be independent of t, at least above some finite value of t (possibly large).
, where δ may depend on t. In order to prove the analyticity in S of the integral in equation (1) it is necessary to show that δ(t) may be chosen to be independent of t, at least above some finite value of t (possibly large).