No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let p = 1 + 5n be a rational prime congruent to 1 (mod 5). Let ζ = e2πi/p and let g be a primitive root mod p. Let the non-zero residues g, g2, …, gp-1 (mod) p be divided into five classes 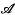 , ℬ,
, ℬ, 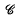 ,
, 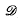 , ℰ, where gν ∈
, ℰ, where gν ∈ 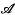 , ℬ,
, ℬ, 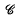 ,
, 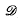 , ℰ according as ν ≡ 0, 1, 2, 3, 4 (mod 5). Let
, ℰ according as ν ≡ 0, 1, 2, 3, 4 (mod 5). Let
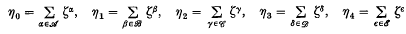
be the 5-nomial periods. Then it is well known (see (3)) that they are the roots of a monic polynomial with integral coefficients. Our object is to determine these coefficients in terms of the quantities A, B, C, D, E, Y, Z considered in a previous paper (2), p. 65. A large number of relations connecting these quantities have been obtained in the above-mentioned paper and we shall use these relations to simplify the coefficients and get them in a reasonably compact and symmetrical form.