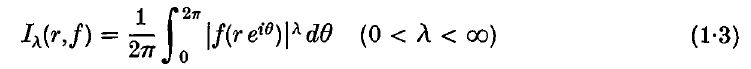Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hansen, Lowell J.
and
Hayman, W. K.
1976.
On the growth of functions omitting large sets.
Journal d'Analyse Mathématique,
Vol. 30,
Issue. 1,
p.
208.
Hayman, W. K.
Patterson, S. J.
and
Pommerenke, Ch.
1977.
On the coefficients of certain automorphic functions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 82,
Issue. 3,
p.
357.
Essén, Matts
1977.
An estimate of harmonic measure in Ṟd, d ≧ 2.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 78,
Issue. 1-2,
p.
129.
Hayman, W. K.
1977.
Complex Analysis.
Vol. 599,
Issue. ,
p.
68.
Baernstein, Albert
and
Rochberg, Richard
1977.
Means and coefficients of functions which omit a sequence of values.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 81,
Issue. 1,
p.
47.
Essén, Matts
1981.
On analytic functions which are in Hp for some positive p.
Arkiv för Matematik,
Vol. 19,
Issue. 1-2,
p.
43.
Hinkkanen, A.
1988.
Holomorphic Functions and Moduli I.
Vol. 10,
Issue. ,
p.
79.
Hinkkanen, A.
1988.
Modulus of continuity of harmonic functions.
Journal d'Analyse Mathématique,
Vol. 51,
Issue. 1,
p.
1.
1989.
Subharmonic Functions.
p.
865.
Betsakos, Dimitrios
2001.
Geometric Theorems and Problems for Harmonic Measure.
Rocky Mountain Journal of Mathematics,
Vol. 31,
Issue. 3,
Karafyllia, Christina
2021.
On a Property of Harmonic Measure on Simply Connected Domains.
Canadian Journal of Mathematics,
Vol. 73,
Issue. 2,
p.
297.