Montel's theorem for subharmonic functions and solutions of partial differential equations
Published online by Cambridge University Press: 24 October 2008
Extract
1. A theorem of Montel (14), states that if f(z) is analytic and bounded in the half-strip
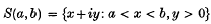
and if there exists an x0 in (a, b) such that

as y → ∞, then

as y → ∞ l. u. on (a, b)(locally uniformly on (a, b), i.e. uniformly on every compact subset of (a, b)). Bohr (3), has proved a version of this result applicable to functions analytic, but not necessarily bounded, in S(a, b) and Hardy, Ingham and Pólya (10), have considered whether or not f(z) can be replaced by |f(z)| in (1·1) and (1·2). They show that this is not so but prove that if f(z) is analytic and bounded in S(a, b) and if
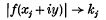
as y → ∞ for three distinct values x1, x2 and z3 in (a, b) then there exist constants A and B such that

as y → ∞, l.u. on (a, b). Cartwright (Theorem 5, (6)) has proved that if f(z) is analytic and satisfies |f(z)| < 1 in, S(a, b) and if for some x0 in (a, b)

asy → ∞, then

as y → ∞ co, l.u. on (a, b) and Bowen (5), has shown that if (1·4) is replaced by the weaker condition
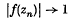
as n → ∞ for some suitable sequence of points Zn in S(a, b) then (1·5) is still valid. In sections 2–5 of this paper we shall consider whether or not these results are valid |f(z)| is replaced by a subharmonic function.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 69 , Issue 1 , January 1971 , pp. 123 - 150
- Copyright
- Copyright © Cambridge Philosophical Society 1971
References
REFERENCES
- 7
- Cited by


