Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cryer, Colin W.
1973.
The LU-factorization of totally positive matrices.
Linear Algebra and its Applications,
Vol. 7,
Issue. 1,
p.
83.
Jacobson, D.H.
1974.
Factorization of symmetric M-matrices.
Linear Algebra and its Applications,
Vol. 9,
Issue. ,
p.
275.
Cryer, Colin W.
1976.
Some properties of totally positive matrices.
Linear Algebra and its Applications,
Vol. 15,
Issue. 1,
p.
1.
Jacobson, D. H.
1976.
A GENERALIZATION OF FINSLER'S THEOREM FOR QUADRATIC INEQUALITIES AND EQUALITIES.
Quaestiones Mathematicae,
Vol. 1,
Issue. 1,
p.
19.
1977.
Extensions of Linear-Quadratic Control, Optimization and Matrix Theory.
Vol. 133,
Issue. ,
p.
73.
Gray, L.J.
and
Wilson, D.G.
1980.
Nonnegative factorization of positive semidefinite nonnegative matrices.
Linear Algebra and its Applications,
Vol. 31,
Issue. ,
p.
119.
Khursheed, Alam
and
Lai Saxena, K. M.
1981.
Positive dependence in multivariate distributions.
Communications in Statistics - Theory and Methods,
Vol. 10,
Issue. 12,
p.
1183.
Rüschendorf, Ludger
1981.
Characterization of dependence concepts in normal distributions.
Annals of the Institute of Statistical Mathematics,
Vol. 33,
Issue. 3,
p.
347.
Ycart, Bernard
1982.
Extrémales du cône des matrices de type non négatif, à coefficients positifs ou nuls.
Linear Algebra and its Applications,
Vol. 48,
Issue. ,
p.
317.
Hannah, John
and
Laffey, Thomas J.
1983.
Nonnegative factorization of completely positive matrices.
Linear Algebra and its Applications,
Vol. 55,
Issue. ,
p.
1.
Hadeler, K.P.
1983.
On copositive matrices.
Linear Algebra and its Applications,
Vol. 49,
Issue. ,
p.
79.
Kaykobad, M.
1987.
On nonnegative factorization of matrices.
Linear Algebra and its Applications,
Vol. 96,
Issue. ,
p.
27.
Berman, Abraham
and
Grone, Robert
1988.
Bipartite completely positive matrices.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 103,
Issue. 2,
p.
269.
Berman, Abraham
1988.
Complete positivity.
Linear Algebra and its Applications,
Vol. 107,
Issue. ,
p.
57.
Berman, Abraham
1993.
Combinatorial and Graph-Theoretical Problems in Linear Algebra.
Vol. 50,
Issue. ,
p.
229.
Bomze, Immanuel M.
2000.
Optimization, Dynamics, and Economic Analysis.
p.
1.
Xu, Changqing
2004.
Completely positive matrices.
Linear Algebra and its Applications,
Vol. 379,
Issue. ,
p.
319.
Sra, Suvrit
2008.
Block-Iterative Algorithms for Non-negative Matrix Approximation.
p.
1037.
Shaked-Monderer, Naomi
2009.
A note on upper bounds on the cp-rank.
Linear Algebra and its Applications,
Vol. 431,
Issue. 12,
p.
2407.
Kalofolias, V.
and
Gallopoulos, E.
2012.
Computing symmetric nonnegative rank factorizations.
Linear Algebra and its Applications,
Vol. 436,
Issue. 2,
p.
421.


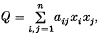 with
with