1. Jurkat and Peyerimhoff(3) (or see (4), pages 50–56) have given a definition of a function, f(A), of an infinite matrix A = (ank). In particular, they considered Aα, where a is any real constant. This is defined wherever A is normal; that is to say, when ank = 0 for k > n, and when, for all n, ann ±0. They also defined the ‘Cesàro iteration’ Aα. This is obtained by defining a matrix B = (bnn) by

(so that every diagonal element of B is 1), forming Bα, and then dividing each row by the row sum; that is to say, if Bα = (b(α)nk), we take

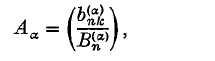
where

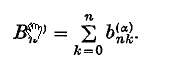
The definition requires, of course, that 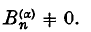≠ 0.