Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T07:42:58.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Boolean algebras in a localic topos

Published online by Cambridge University Press:  24 October 2008

B. Banaschewski  and
K. R. Bhutani
B. Banaschewski
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, Ont. L8S 4KI, Canada
K. R. Bhutani
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, Ont. L8S 4KI, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

When a familiar notion is modelled in a certain topos E, the natural problem arises to what extent theorems concerning its models in usual set theory remain valid for its models in E, or how suitable properties of E affect the validity of certain of these theorems. Problems of this type have in particular been studied by Banaschewski[2], Bhutani[5], and Ebrahimi[6, 7], dealing with abelian groups in a localic topos and universal algebra in an arbitrary Grothendieck topos. This paper is concerned with Boolean algebras, specifically with injectivity and related topics for the category 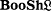of Boolean algebras in the topos 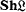of sheaves on a locale 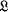and with properties of the initial Boolean algebra in .

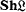Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 100 , Issue 1 , July 1986 , pp. 43 - 55
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balbes, R. and Dwinger, P.. Distributive Lattices (University of Missouri Press, 1975).Google Scholar
[2]Banaschewski, B.. When are divisible abelian groups injective? Quaest. Math. 4 (1981), 285–307.CrossRefGoogle Scholar
[3]Banaschewski, B. Injectivity and modelling in the Blass topos. Unpublished manuscript.Google Scholar
[4]Bell, J. L.. On the strength of the Sikorski Extension Theorem for Boolean algebras. J. Symbolic Logic 48 (1983), 841–846.CrossRefGoogle Scholar
[5]Bhutani, K. R.. Abelian groups in a topos of sheaves on a locale. Doctoral dissertation, McMaster University, 1983.Google Scholar
[6]Ebrarimi, M.. Algebra in a topos of sheaves. Doctoral dissertation, McMaster University, 1980.Google Scholar
[7]Ebrahimi, M.. Algebra in a Grothendieck topos: Injectivity in quasiequational classes (To appear.)Google Scholar
[8]Fourman, M. P. and Scott, D. S.. Sheaves and logic. Applications of Sheaves, Proceedings, Durham 1977. Lecture Notes in Mathematics, vol. 753 (Springer-Verlag, 1979), 302–401.CrossRefGoogle Scholar
[9]Halmos, P.. Lectures on Boolean Algebras (Van Nostrand, 1963).Google Scholar
[10]Halpern, J. D.. The independence of the axiom of choice from the Boolean prime ideal theorem. Fund. Math. 55 (1964), 57–66.CrossRefGoogle Scholar
[11]Johnstone, P. T.. Topos Theory (Academic Press, 1977).Google Scholar
[12]Johnstone, P. T.. Conditions related to de Morgan's law. Applications of sheaves, Proceedings, Durham 1977. Lecture Notes in Mathematics vol. 753 (Springer-Verlag, 1979), 479–491.CrossRefGoogle Scholar
[13]Johnstone, P. T.. Another condition equivalent to de Morgan's law. Commun. Alg. 7 (1979), 1309–1312.CrossRefGoogle Scholar
[14]Johnstone, P. T.. The Gleason cover of a topos. I. J. Pure Appl. Alg. 19 (1979), 171–192.CrossRefGoogle Scholar
[15]Johnstone, P. T.. Stone Spaces. Cambridge Studies in Advanced Mathematics no. 3 (Cambridge University Press, 1982).Google Scholar
[16]Lane, S. Mac. Categories for the Working Mathematician. Graduate Texts in Mathematics, no. 5 (Springer-Verlag, 1971).CrossRefGoogle Scholar
[17]Sikorski, R.. Boolean Algebras. Ergebnisse der Math. Band 25 (Springer-Verlag, 1964).Google Scholar