Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T06:06:58.699Z Has data issue: false hasContentIssue false
  • English
  • Français

On the computation of the determinant of vector-valued Siegel modular forms

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 August 2014

Sho Takemori
Sho Takemori*
Affiliation:
Department of Mathematics, Kyoto University, Kitashirakawa-Oiwake-Cho, Sakyo-Ku, Kyoto, 606-8502, Japan email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 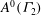$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}A^{0}(\Gamma _{2})$ denote the ring of scalar-valued Siegel modular forms of degree two, level 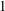$1$ and even weights. In this paper, we prove the determinant of a basis of the module of vector-valued Siegel modular forms 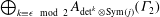$\bigoplus _{k \equiv \epsilon \ {\rm mod}\ {2}}A_{\det ^{k}\otimes \mathrm{Sym}(j)}(\Gamma _{2})$ over 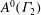$A^{0}(\Gamma _{2})$ is equal to a power of the cusp form of degree two and weight $35$ up to a constant. Here 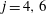$j = 4, 6$ and 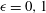$\epsilon = 0, 1$. The main result in this paper was conjectured by Ibukiyama (Comment. Math. Univ. St. Pauli 61 (2012) 51–75).

MSC classification

Secondary: 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms 11F03: Modular and automorphic functions 11F11: Holomorphic modular forms of integral weight 11F60: Hecke-Petersson operators, differential operators (several variables)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 247 - 256
Copyright
© The Author 2014 

References

Aoki, H. and Ibukiyama, T., ‘Simple graded rings of Siegel modular forms, differential operators and Borcherds products’, Int. J. Math. 16 (2005) no. 3, 249–279.CrossRefGoogle Scholar
Arakawa, T., ‘Vector valued Siegel’s modular forms of degree two and the associated Andrianov L-functions’, Manuscripta Math. 44 (1983) no. 1–3, 155–185.CrossRefGoogle Scholar
Choi, D., Choie, Y. and Kikuta, T., ‘Sturm type theorem for Siegel modular forms of genus 2 modulo p’, Acta Arith. 158 (2013) no. 2, 129–139.CrossRefGoogle Scholar
Eholzer, W. and Ibukiyama, T., ‘Rankin–Cohen type differential operators for Siegel modular forms’, Int. J. Math. 9 (1998) no. 4, 443–463.CrossRefGoogle Scholar
Eisenbud, D., Commutative algebra: with a view toward algebraic geometry, Graduate Texts in Mathematics vol. 150 (Springer, 1995).CrossRefGoogle Scholar
Ibukiyama, T., ‘On differential operators on automorphic forms and invariant pluri-harmonic polynomials’, Comment. Math. Univ. St. Pauli 48 (1999) no. 1, 103–118.Google Scholar
Ibukiyama, T., ‘Vector valued Siegel modular forms of symmetric tensor weight of small degrees’, Comment. Math. Univ. St. Pauli 61 (2012) 51–75.Google Scholar
Igusa, J., ‘On Siegel modular forms of genus two’, Amer. J. Math. (1962) 175–200.Google Scholar
Kiyuna, T., ‘Vector-valued Siegel modular forms of weight $\det ^{k}{\otimes }\, \mathrm{Sym}(8)$’, Preprint, 2013.Google Scholar
Klingen, H., ‘Zum Darstellungssatz für Siegelsche Modulformen’, Math. Z. 102 (1967) no. 1, 30–43.Google Scholar
Satoh, T., ‘On certain vector valued Siegel modular forms of degree two’, Math. Ann. 274 (1986) no. 2, 335–352.CrossRefGoogle Scholar
Stein, W. A. et al. , Sage Mathematics Software (Version 6.1.1), The Sage Development Team, 2014,http://www.sagemath.org.Google Scholar
Tsushima, R., ‘An explicit dimension formula for the spaces of generalized automorphic forms with respect to Sp(2, Z)’, Proc. Japan Acad. Ser. A Math. Sci. 59 (1983) no. 4, 139–142.CrossRefGoogle Scholar
van Dorp, C. H., ‘Generators for a module of vector-valued Siegel modular forms of degree 2’, Preprint, 2013, arXiv:1301.2910.Google Scholar