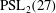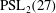Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wilson, Robert A.
2015.
Every in the Monster contains -elements.
LMS Journal of Computation and Mathematics,
Vol. 18,
Issue. 1,
p.
667.
Wilson, Robert A.
2016.
Is the Suzuki group Sz(8) a subgroup of the Monster?.
Bulletin of the London Mathematical Society,
Vol. 48,
Issue. 2,
p.
355.
Wilson, Robert A.
2017.
The uniqueness of PSU 3(8) in the Monster.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 5,
p.
877.
Kelsey, Veronica
and
Rowley, Peter
2020.
A note on involution centralizers in black box groups.
Journal of Group Theory,
Vol. 23,
Issue. 2,
p.
287.
Dietrich, Heiko
Lee, Melissa
and
Popiel, Tomasz
2025.
The maximal subgroups of the Monster.
Advances in Mathematics,
Vol. 469,
Issue. ,
p.
110214.