Journal of the Staple Inn Actuarial Society, Volume 8 - 1949
- This volume was published under a former title. See this journal's title history.
Research Article
Methods of bonus distribution with special reference to the reduction of premium system
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 1-19
-
- Article
- Export citation
Disability benefits in conjunction with life assurance policies
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 121-146
-
- Article
- Export citation
Computing methods
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 65-77
-
- Article
- Export citation
Depreciation allowances in the valuation of reversions
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 196-203
-
- Article
- Export citation
A nomogram for calculating extended terms
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 147-159
-
- Article
- Export citation
Valuation for Estate Duty purposes of an estate subject to an annuity
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 78-81
-
- Article
- Export citation
On the mathematical theory of risk
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 20-37
-
- Article
- Export citation
Discrete random Processes*
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 204-209
-
- Article
- Export citation
Mathematics and the actuary
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 160-175
-
- Article
- Export citation
Medical examination for contingent assurances
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 210-215
-
- Article
- Export citation
Notes on valuations for Estate Duty purposes
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 82-86
-
- Article
- Export citation
Tests of significance in the simple regression problem
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 38-43
-
- Article
- Export citation
The conversion of whole life extras into extra premiums for other classes of assurance
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 176-185
-
- Article
- Export citation
On the application of compound interest functions to certain manpower problems
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 44-48
-
- Article
- Export citation
The use of normal significance limits when the parent population is of Laplace form
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 87-99
-
- Article
- Export citation
The nomographic estimation of the influence of substandard mortality on the policy value
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 216-223
-
- Article
- Export citation
The application of the Service-Table technique to staffing problems
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 49-55
-
- Article
- Export citation
Other
Award of prize
-
- Published online by Cambridge University Press:
- 11 August 2014, p. 224
-
- Article
- Export citation
Research Article
Annuities certain at linearly decreasing rates of interest
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 186-189
-
- Article
- Export citation
Sheppard's correction to the variance
-
- Published online by Cambridge University Press:
- 11 August 2014, pp. 100-103
-
- Article
- Export citation

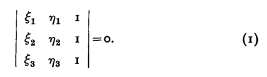
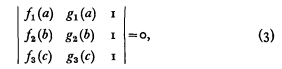
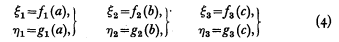
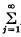
 where
where  and
and . This is a function of
. This is a function of 

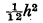 from the calculated variance. This note gives an interpretation in elementary terms of the ‘reason’ for such a correction.
from the calculated variance. This note gives an interpretation in elementary terms of the ‘reason’ for such a correction.