Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T12:32:59.352Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete random Processes*

Published online by Cambridge University Press:  11 August 2014

Get access

Extract

If a variable assumes the discrete values xj (j = 1, 2, 3, …) with specified probabilities f(xj), where 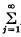f(xj) it is said to be a discrete random variable. If a discrete random variable is also a function of a continuous (non-random) variable, for convenience usually assumed to be ‘time’, it is called a discrete random process.

A class of discrete random processes of particular interest to the pure mathematician and to the mathematical statistician has been called stochastically definite by Kolmogoroff (1931). Such a random process is distinguished by the fact that the probability that the random variable concerned assumes a given value n at time t depends only on the value m assumed by the variable at time s (s < t) and not on the values assumed at any intermediate or earlier points of time. This circumstance is allowed for by writing the probability of the value n at time t in the form Pmn (s, t).

Type
Research Article
Information
Journal of the Staple Inn Actuarial Society , Volume 8 , Issue 4 , 1949 , pp. 204 - 209
Copyright
Copyright © Institute of Actuaries Students' Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Being the substance of a contribution to the University of Toronto's mathematical colloquium held on 12 October 1948.

References

REFERENCES

Ackermann, W.-G. (1939). Eine Erweiterung des Poissonschen Grenzwertsatzes und ihre Anwendung auf die Risikoprobleme in der Sachversicherung. Schriften des Math. Inst. u. des Inst. f. angew. Math. d. Univ. Berlin.Google Scholar
Campagne, C., Jongh, B. H. de & Smit, J. N. (1947). Bijdrage tot de wiskundige theorie van de bedrijfsreserve en het eigenbehoud in de brandverzekering. 's Gravenhage.Google Scholar
Cantelli, F. P. (1942). I fondamenti matematici della tecnica delle assicurazioni. G. Ist. ital. Attuari, XIII, 1.Google Scholar
Cramer, H. (1927). Sannolikhetskalkyien och nägra av dess användningar. Stockholm.Google Scholar
Dubourdieu, J. (1938). Remarques relatives à la théorie mathématique de l'assurance-accidents. Bull. Inst. Actu. franç. XLIX, 79.Google Scholar
Feller, W. (1936). Zur Theorie der stochastischen Prozesse. Math. Ann. CXIII, 113.Google Scholar
Fréchet, M. (1938). Recherches théoriques modernes sur le calcul des probabilités, vol. II. Paris.Google Scholar
Fry, T. C. (1928). Probability and its Engineering Uses. New York.Google Scholar
Greenwood, M. & Yule, G. U. (1920). An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or of repeated accidents. J. Roy. Statist. Soc. LXXXIII, 255.Google Scholar
Hadwiger, H. (1945). Über Verteilungsgesetze vom Poissonschen Typus. Mitt. Verein. schweiz. Vers.-Mathr. XLV, 257.Google Scholar
Hostinsky, B. (1931). Méthodes générales du calcul des probabilités. Mém. Sci. Math. LII.Google Scholar
Khintchine, A. (1933). Asymptotische Gesetze der Wahrscheinlichkeitsrechnung. Berlin.Google Scholar
Kolmogoroff, A. (1931). Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung. Math. Ann. CIV, 415.Google Scholar
Lundberg, F. (1919). Teori för riskmassor. Stockholm.Google Scholar
Lundberg, O. (1940). On Random Processes and their Application to Sicknes and Accident Statistics. Uppsala.Google Scholar
Riebesell, P. (1941). Die mathematischen Grundlagen der Sachversicherung. Ber. XII. Int. Kongr. Versich.-Math. Luzern, 1940, IV, 27.Google Scholar
Satterthwaite, F. E. (1942). Generalized Poisson distribution. Ann. Math. Statist, XIII, 410.Google Scholar
Seal, H. L. (1945). Contribution to discussion on Elderton's ‘Cricket scores and some skew correlation distributions’. J. Roy. Statist. Soc. CVIII, 1.Google Scholar
Seal, H. L. (1948). The probability of decrements from a population. A study in discrete random processes. Skand. Aktuar Tidskr. XXI, 14.Google Scholar
Vajda, S. (1948). Statistical investigation of casualties suffered by certain types of vessels. Suppl.J. R. Statist. Soc. IX, 141.Google Scholar