Reviews
Computability, enumerability, unsolvability, Directions in recursion theory, edited by S. B. Cooper, T. A. Slaman, and S. S. Wainer, London Mathematical Society lecture note series, no. 224, Cambridge University Press, Cambridge, New York, and Oakleigh, Victoria, 1996, vii + 347 pp. - Leo Harrington and Robert I. Soare, Dynamic properties of computably enumerable sets, Pp. 105–121. - Eberhard Herrmann, On the ∀∃-theory of the factor lattice by the major subset relation, Pp. 139–166. - Manuel Lerman, Embeddings into the recursively enumerable degrees, Pp. 185–204. - Xiaoding Yi, Extension of embeddings on the recursively enumerable degrees modulo the cappable degrees, Pp. 313–331. - André Nies, Relativization of structures arising from computability theory. Pp. 219–232. - Klaus Ambos-Spies, Resource-bounded genericity. Pp. 1–59. - Rod Downey, Carl G. Jockusch, and Michael Stob. Array nonrecursive degrees and genericity, Pp. 93–104. - Masahiro Kumabe, Degrees of generic sets, Pp. 167–183. - Marat M. Arslanov, Steffen Lempp, and Richard A. Shore, On isolating r.e. and isolated d-r.e. degrees, Pp. 61–80. - S. Barry Cooper, A characterisation of the jumps of minimal degrees below 0′, Pp. 81–92. - Michael E. Mytilinaios and Theodore A. Slaman, On a question of Brown and Simpson, Pp. 205–218. - Andrew J. Heaton and Stanley S. Wainer. Axioms for subrecursion theories, Pp. 123–138. - Dag Normann, A hierarchy of domains with totality, but without density, Pp. 233–257. - Piergiorgio Odifreddi, Inductive inference of total functions, Pp. 259–288. - Andrea Sorbi, The Medvedev lattice of degrees of difficulty, Pp. 289–312. - S. B. Cooper, T. A. Slaman, and S. S. Wainer, Appendix: questions in recursion theory, Pp. 333–347.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1362-1365
-
- Article
- Export citation
Research Article
Classification of δ-invariant amalgamation classes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1743-1750
-
- Article
- Export citation
Reviews
John P. Burgess and Gideon Rosen, A subject with no object. Strategies for nominalistic interpretation of mathematics, Clarendon Press, Oxford University Press, Oxford and New York1997, xi + 259 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 391-394
-
- Article
- Export citation
Research Article
Generic expansions of ω-categorical structures and semantics of generalized quantifiers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 775-789
-
- Article
- Export citation
Notions of locality and their logical characterizations over finite models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1751-1773
-
- Article
- Export citation
Reviews
Penelope Maddy. Naturalism in mathematics. Clarendon Press, Oxford University Press, Oxford and New York1998 (© 1997), ix + 254 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 394-396
-
- Article
- Export citation
Research Article
The finite model property for various fragments of intuitionistic linear logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 790-802
-
- Article
- Export citation
Reviews
Vladimir Kanovei and Michael Reeken, Internal approach to external sets and universes, Part 1, Bounded set theory, Studia logica, vol. 55 (1995), pp. 229–257. - Vladimir Kanovei and Michael Reeken, Internal approach to external sets and universes, Part 2, External universes over the universe of bounded set theory, Studia logica, vol. 55 (1995), pp. 347–376. - Vladimir Kanovei and Michael Reeken, Internal approach to external sets and universes, Part 3, Partially saturated universes, Studia logica, vol. 56 (1996), pp. 293–322.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1365-1366
-
- Article
- Export citation
Research Article
The complexity of decision procedures in relevance logic II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1774-1802
-
- Article
- Export citation
Reviews
The Columbia history of western philosophy, edited by Richard H. Popkin, Columbia University Press, New York1999, xxvi + 836 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 396
-
- Article
- Export citation
Martin Goldstern and Haim Judah, The incompleteness phenomenon, A new course in mathematical logic, A K Peters, Wellesley, Mass., 1995, xiii + 247 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1367-1368
-
- Article
- Export citation
Research Article
Stabilité polynômiale des corps différentiels
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 803-816
-
- Article
- Export citation
Reviews
Geoffrey Hellman. Constructive mathematics and quantum mechanics: unbounded operators and the spectral theorem. Journal of philosophical logic, vol. 22 (1993), pp. 221–248.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 397-398
-
- Article
- Export citation
Research Article
Lascar strong types in some simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 817-824
-
- Article
- Export citation
Reviews
Patrick Suppes, Introduction to logic. A republication of XXII 353 Publications, Mineola, New York, 1999, xiv + 312 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 1368
-
- Article
- Export citation
Research Article
Adjoining cofinitary permutations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1803-1810
-
- Article
- Export citation
Reviews
Wilfried Sieg. Step by recursive step: Church's analysis of effective calculability. The bulletin of symbolic logic, vol. 3 (1997), pp. 154–180.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 398-399
-
- Article
- Export citation
Research Article
Existentially closed models of the theory of artinian local rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 825-845
-
- Article
- Export citation
Reviews
Lewis Carroll (pseudonym), Das Spiel der Logik, Germam Translation by Micheal Zöllner of 671, Edited and with an afterword by Paul Good. Tropen Verlag, Cologne, and Frommann-Holzboog, Stuttgart, 1998, 199 pp. - Paul Good, Logik—ein Spiel, Therein, pp. 103–119.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1368-1370
-
- Article
- Export citation
Research Article
Some results on combinators in the system TRC
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1811-1819
-
- Article
- Export citation

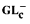 of Ono [11], that will settle the open problems stated in Ono [12].
of Ono [11], that will settle the open problems stated in Ono [12].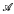
 o
o