The notion of a hyperfinite set comes from nonstandard analysis. Such a set has the internal cardinality of a nonstandard natural number. By a transfer principle such sets share many properties of finite sets. Here we apply this notion to give a hyperfinite model of the Kleene-Kreisel continuous functionals. We also extend the method to provide a hyperfinite characterisation of certain transfinite type structures, thus, through the work of Waagbø [14], constructing a hyperfinite model for Martin-Löf type theory.
This kind of application is not new. Normann [6] gave a characterisation of the Kleene-Kreisel continuous functionals using ‘hyperfinitary’ functionals. The novelty here is that we use a constructive version of hyperfinite functionals and also generalise the method to transfinite types. Many of the results of this paper are constructive, though not the characterisation theorems themselves.
Our characterisation of the Kleene-Kreisel continuous functionals is a supplement to a number of previous characterisations of topological and recursion-theoretical nature, see [6] for a brief survey. Altogether these characterisations show that the original concept of Kleene and Kreisel forms the correct mathematical model of the idea of finitely based functions of finite types.
There is, however, no a priori reason to believe that there is a canonical way to extend the continuous functionals to cover transfinite objects of transfinite type used in, e.g., type theory. Our characterisation of Waagbø's model indicates that the model is natural, not only seen from domain theory but from a higher perspective. Normann and Waagbø (unpublished) have subsequently obtained a limit-space characterisation that further supports this view.
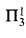 sets and
sets and 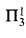 singletons
singletons