The aim of this paper is to present a decision procedure which seems to be as easy to use as other available procedures in quantification theory, but which is considerably stronger than the others, providing a mechanical test for a sub-species of polyadic validity which is very much broader than monadic validity. Of course, a test for polyadic validity in general is out of the question, but the present test's limits, short of polyadic validity, are not known. That is, of all the polyadically valid schemata which have been tested, ncne has failed to yield decisions under this method. The material thus examined includes schemata corresponding to the cases of all absolute metatheorems in ML's Chapters II and III, and five polyadic samples from MeL. The handiness of this test is illustrated by sample applications in § 3 below.

By a logical measure (for a given language) we mean a syntactically defined function which associates some value with each well-formed formula of the language. Various such logical measures have played a fundamental role in the development of Logic and the Philosophy of Science. The purpose of this paper is to define a logical measure which has much wider applications than measures so far studied.

The new measure has two fundamental advantages, which will be referred to throughout the paper. First of all it can be applied to more (and richer) languages than the older measures. Most of the measures now in use are restricted to the first-order functional calculus, and frequently even to a first-order calculus with one-place predicates only. The measure to be defined will be applicable to richer languages as well, e.g., to functional calculi of all finite orders. But even as far as the first-order functional calculus is concerned, the new measure has a great advantage: We do not have to require that the atomic sentences of the calculus be independent. The previous measures depended in their construction on the requirement that “the basic statements of the language express independent facts.”

By an atomic sentence we mean a well-formed formula formed by applying an h-place primitive predicate to h individuals (a well-formed formula no part of which is well-formed); by a permissible conjunction we mean a conjunction of atomic sentences and negations of other atomic sentences; and the requirement of independence is that an atomic sentence (or its negation) is logically implied by a permissible conjunction only if it (its negation) is one of the components of the conjunction.

It is well-known that every involution in a logical or mathematical system gives rise to a theory of duality; for example, negation in the sentential calculus and predicate calculus, complementation in the calculus of classes, complementation and conversion in the calculus of relations, etc. The purpose of this note is to call attention to the fact that every involution in a logical or mathematical system gives rise to a theory of quaternality and that the square of quaternality, of which the classical squares of opposition are special cases, provides a diagrammatic representation for much of the theory of quaternality. For the sake of definiteness we expose the theory of quaternality in the context of the lower predicate calculus.

Let ϕ and ψ be formulas of the lower predicate calculus. The constants {T and F} {∧ and ∨} {→ and ⇷} {← and ⇸}{↔ and ⇹} {↑ and ↓} {∧ (all) and ∨ (some)} are dual. The constant ~ is self-dual. The negational of ϕ, denoted ϕN, is the formula obtained from ϕ by interchanging negated and unnegated variables (that is, sentence variables and predicate variables) and by interchanging dual constants. The contradual of ϕ, denoted ϕC, is the formula obtained from ϕ by interchanging negated and unnegated variables. The dual of ϕ, denoted ϕD, is the formula obtained from ϕ by interchanging dual constants. The four formulas ϕ, ϕN, ϕC, ϕD, are quaternals of each other.

In [3] Myhill has constructed a complete system K which allows in it the development of a large and important section of classical mathematics. Completeness is achieved essentially by sacrificing universal quantification and introducing instead the proper ancestral as a primitive idea.

In the following we are presenting a system K0 which will be shown to be equivalent to K (i.e. the primitive operators of both systems are mutually definable in terms of one another). K0 is also complete and covers the same ground as K. K0, however, differs from K by the introduction of the limited universal quantifier instead of the proper ancestral and of concatenation instead of the ordered-pair function as primitive operators. By a further reduction K0 will be shown to be equivalent to the system K1 not containing the abstraction-operator and the class-membership relation.

In a recent paper by Mostowski [1] we find an investigation of those formulas of quantification theory which are valid in all domains of individuals, including the empty domain. Mostowski gives a complete set of axioms for such a first order functional calculus (the system is called “”) and a comparison is made with a form of the usual calculus, Church's in [2]. It is pointed out that is much less elegant; in particular, the distributivity laws for quantifiers (e.g., (x){A . B) .{x)A . (x)B) do not hold in general, and likewise the rule of modus ponens does not preserve validity in all cases.

In this paper we show that a not inelegant system is obtained if one modifies Mostowski's approach in two respects; and once this is done a somewhat neater proof of completeness can be given.

The first respect in which we diverge from Mostowski is in the treatment of vacuous quantifiers. For him if p has no free x, then (x)p and (∃x)p are both to have the same value (interpretation) as p1. But this is not the only way to assign values to vacuous quantifications. For when universal quantification is viewed as a generalized conjunction, the formula (x)Fx has the significance of Fa . Fb…. for as many conjunctands as there are individuals in the domain, and if Fx should have the “constant” value p, then (x)p is to mean the conjunction of p with itself for as many times as there are individuals in the domain (compare the arithmetical ).

There occurs in Aristotle a thesis which is symbolised in I. M. Bocheński's La Logique de Théophraste, Chapter V, by the formula EMpMNp. We might read this as “It is possible that P (Mp) if and only if (E) it is possible that not P (MNp).” But as Bocheński explains, Aristotle is here using the word “possible” to mean, not merely “not impossible”, but “neither necessary nor impossible”. And if we take “ It is impossible that P” to mean “It is necessary that not P”, Aristotle's thesis seems evidently true. For “It is neither necessary nor impossible that P” (Mp) amounts to “It is not necessary that P, and it is not necessary that not P” (KNSpNSNp, where S is the symbol for “It is necessary that”); and “It is neither necessary nor impossible that not P” (MNp) amounts to “It is not necessary that not P, and it is not necessary that not not P” (KNSNpNSNNp); and this reduces easily to the other by the law of double negation (ENNpp) and the commutativeness of conjunction (EKpqKqp).

Despite the apparently unexceptionable character of this thesis EMpMNp, when properly understood, Bocheński informs us, in paragraph 42 of this chapter, that Łukasiewicz has shown that it “implies a contradiction”. He goes on to explain that what he means by this is that it follows from this thesis, together with the assumption that some propositions are “possible” in the Aristotelian sense, that any proposition whatever is “possible” (in that sense). And this, when one thinks what it means, is a most extraordinary contention.

Axiomatizations of two systems of modal logic are presented in this paper. The first consists of six axiom schemata and one rule of inference; this axiomatization is proved equivalent to Lewis' S3. The addition of a seventh schema, the analogue of C10. 1, yields an axiomatization equivalent to S4. Our axiom schemata for S3 are proved mutually independent, as are our schemata for S4.

The purpose of this paper is to prove two theorems and a conjecture (Conjecture II) announced in section 15 an earlier paper of the author's (cited as “CT”), and to compare them briefly with related results of Specker. Familiarity with both papers is assumed; the terminology of the former is used throughout. On two points however clarification of the usage of CT is in order, and to this chore we must first proceed.

A half-section is the lower half of a Dedekind cut; if the cut is rational, the half section is to include the rational corresponding to the real defined by the cut. A whole-section is the relation which holds between any member of the lower and any member of the upper half of some Dedekind cut. If the cut is rational the corresponding rational is to be a member of both halves.

A real number α is said to be approximate in K to any required number of decimal places if it is possible to define the predicates ‘x < α’, ‘x ≤ α’, ‘x > α’, and ‘x ≥ α’ (x rational) in K. In view of section 7 of CT this will mean that every true inequation between α and a terminating decimal will be provable in K.

If we think of denotation in a broad sense, we may say not only that, e.g., ‘Marni’ denotes the actual dog Marni but also that ‘dog’ denotes severally the dogs Marni, Fido, etc. What are ordinarily called class names thus come to denote severally the members of the class but not the class itself. This kind of a multiple denotation relation is a very simple as well as a very powerful semantical relation. In fact it can be taken as the fundamental relation of formal (extensional) semantics.

Conceptually this denotation relation is akin to the relation of satisfaction studied by Tarski, although the two must be carefully distinguished. Satisfaction (in its simplest form) is a relation between objects and sentential functions of one variable. Denotation is taken as a relation holding, on the one hand, between what is ordinarily called a proper name and the object which it names, and, on the other, between what may be called a virtual class denotator and the objects which are members of the virtual class in question. (This relation will be characterized more precisely below.) Clearly the two relations, satisfaction in its simplest form and multiple denotation, are interdefinable in an appropriate formalism.

Let and be (well-formed) formulas of the functional calculus, let c be an n-adic functional variable, and let a1, …, an be distinct individual variables. Church has defined the metalogical notation to indicate the formula resulting from when each part of of the form c{1, …, n) (such that the occurrence of c is free in ) is replaced by the formula which arises from by replacing every free occurrence of ai by i, i, = 1, …, n. (Here 1, …, n may be any individual variables or constants, not necessarily all distinct.) The notation is not defined for all , , c, a1, …, an, however, but only for those cases (specified in detail by Church) when the resulting formula constitutes a valid substitution instance of the formula according to the standard interpretation of the functional calculus.

The full and correct syntactical statement of the conditions (under which this type of substitution is permissible) has proved so arduous, that it seems to have been rendered in error more often than not. Unfortunately the functional calculi are often set up as deductive systems in which this type of substitution occurs as one of the primitive rules of inference, or in one of the axiom schemata. Thus the beginning student who is introduced to the calculi through such a formulation is forced to cope from the outset with details which have proved treacherous even to the initiate. For this reason it is desirable to seek alternative formulations of the functional calculi in which this type of substitution is not mentioned.

Halldén, in [1], has recently pointed out that it is highly undesirable, in a system of sentential calculus, for there to exist two formulas α and β such that: (i) α and β contain no variable in common; (ii) neither α nor β is provable; (iii) α ∨ β is provable. We shall call a system unreasonable (in the sense of Halldén) if there exists a pair of formulas α and β having properties (i), (ii), and (iii). Halldén shows (in [1]) that the Lewis systems S1 and S3 are unreasonable in this sense; and that the same is true of any system which is between S1 and S3, as well as of every system which is stronger than S3 but weaker than both S4 and S7. In the present note we shall show that this defect does not occur in S4, nor in S5, nor in any “quasi-normal” extension of S5; we give an example, on the other hand, of an unreasonable system which lies between S4 and S5.

When we speak, in what follows, of a system of modal logic, we shall mean a system having the same class of well-formed formulas as have the various Lewis calculi. Thus the well-formed formulas of a system of modal logic, when written in unabbreviated form, are just those formulas which can be built up from sentential variables by use of the binary connective ‘·’ (conjunction sign), and the two unary connectives ‘˜’ (negation sign) and ‘◇’ (possibility sign). We shall, however, also make use of some of the defined signs of Lewis.

The program of “basic logic” can be summarized as follows:

I. To treat every syntactical system as a subclass of a certain fixed infinite classUof “U-expressions.” This can always be done by modifying in trivial ways the notation of each syntactical system which is not already such a subclass. As a result all syntactical systems become comparable with each other in the sense that they are merely different subclasses of a single class of expressions. The class U can be chosen in such a way as to be inductively definable thus in terms of a fixed symbol ‘σ’: (1) The symbol ‘σ’ is a U-expression. (2) The result of placing two U-expressions (or two occurrences of the same U-expression) next to each other, and enclosing this total expression within a pair of parentheses, is a U-expression.

II. To formulate a particular syntactical systemKwithin which every syntactical system (and indeedKitself) is “represented.” Such a system is here said to be a “basic system,” and an appropriate interpretation of it is said to be a “basic logic.” Within such a logic every finitary logic is definable, as well as the basic logic itself. Such a logic should be of fundamental importance, especially if it is so constructed as to be the weakest such logic and so contain no theorems that are not essential to its being basic.

With the above considerations in view, the system K has been defined in such a way that it is a subclass of U and is a basic syntactical system. A simpler definition of K will be given than heretofore in previous papers, and the minimum character of K will be made more clear.

In two papers appearing in successive issues of this Journal, Quine and Goodman, impelled by a philosophical standpoint which forswears all traffic in abstract entities, have explored the possibility of reinterpreting the language of classical mathematics so as to give it meaning (consistent with the observed overt pattern of standard usage) in terms of the narrow domain of entities which they recognize. The present paper offers several comments on this program.

The problem of constructing formal systems involving transfinite types was briefly suggested many times in the literature. Actually few attempts have been made to develop such systems. In particular, there exists a system based on a set of axioms and rules of inference suggested by Church and worked out in detail by E. Bustamante in his dissertation. Recently, John Kemeny has reformulated this system in a simplified way and has obtained an interesting hierarchy of systems. It so happens that all these systems considered by Kemeny may be regarded as successive extensions of a particular formulation of the theory of finite types, namely a certain monadic functional calculus of order ω whose main ideas are due to Tarski.

There exists on the other hand a quite different formulation of the theory of finite types which is due to Church. It is a formulation which incorporates certain features of the calculus of λ-conversion, and which has revealed itself quite advantageous for certain purposes. The formulation of the theory of transfinite types which we are going to introduce in this paper may be considered as an attempt to generalize Church's formulation of the theory of finite types.

A class A for which there is an infinite progression of classes A1, A2, … (not necessarily all distinct) such that

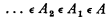
is said to be groundless. A class which is not groundless is said to be grounded. Let K be the class of all grounded classes.

Let us assume that K is a groundless class. Then there is an infinite progression of classes A1, A2, … such that

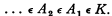
Since A1 ϵ K, A1 is a grounded class; since

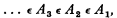
A1 is also a groundless class. But this is impossible.

Therefore K is a grounded class. Hence K ϵ K, and we have

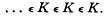
Therefore K is also a groundless class.

This paradox forms a sort of triplet with the paradox of the class of all non-circular classes and the paradox of the class of all classes which are not n-circular (n a given natural number). The last of the three includes as a special case the paradox of the class of all classes which are not members of themselves (n = 1).

More exactly, a class A1 is circular if there exists some positive integer n and classes A2, A3, …, An such that

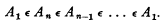
For any given positive integer n, a class A1 is n-circular if there are classes A2, …, An, such that

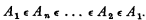
Quite obviously, by arguments similar to the above, we get a paradox of the class of all non-circular classes and a paradox of the class of all classes which are not n-circular, for each positive integer n.

In a recent paper [4] on mean value theorems in recursive function theory we proved the theorem that

(A) iff(n, x) is relatively differentiable with a relative derivative f1(n, x), for a ≤ x ≤ b, and if f(n, a) = f(n, b) = 0 relative to n,

then there is a recursive function ck, a < ck < b, and a recursive R(k) such that f1(n, ck) = 0(k) for n ≥ R(k); and we showed further that the added condition

(B) f(n, x) is either relatively variable or relatively constant

suffices to ensure that ck is uniformly contained in (a, b), i.e. that there exist α, β such that

A comparison with the conditions under which Rolle's theorem is established in classical analysis suggests that clause (A) itself might suffice to ensure that ck is uniformly contained in (a, b); for in the classical theory there is a single point c, a < c < b, for which lim f1(n, c) = 0, and therefore f1(n, c) = 0(k) for sufficiently great values of n, where of course c is independent of k.

The object of the present note is to show that this is not in fact the case, and we shall construct a recursive function f(n, x) satisfying condition (A) in the interval (0, 1) and such that any sequence ck for which f1(n, ck) = 0(k) for large enough values of n is not uniformly contained in (0, 1).

Let C be the closure of a recursively enumerable set B under some relation R. Suppose there is a primitive recursive relation Q, such that Q is a symmetric subrelation of R (i.e. if Q(m, n), then Q(n, m) and R(m, n)), and such that, for each m ϵ B, Q(m, n) for infinitely many n. Then there exists a primitive recursive set A, such that C is the closure under R of A. For proof, note that , where f is a primitive recursive function which enumerates B, has the required properties. For each m ϵ B, there is an n ϵ A, such that Q(m, n) and hence Q(n, m); therefore the closure of A under Q, and hence that under R, includes B. Conversely, since Q is a subrelation of R, A is included in C. Finally, that A is primitive recursive follows from [2] p. 180.

This observation can be applied to many formal systems S, by letting R correspond to the relation of deducibility in S, so that R(m, n) if and only if m is the Gödel number of a formula of S, or of a sequence of formulas, from which, together with axioms of S, a formula with the Gödel number n can be obtained by applications of rules of inference of S.

The purpose of this paper is to present a system of arithmetic stronger than those usually employed, and to prove some syntactical theorems concerning it.

We presuppose the lower functional calculus with identity and functions, and we start with three of Peano's axioms.

The other two (0 ϵ N and x ϵ N .⊃. x′ ϵ N) we do not need since our variables are anyhow restricted to natural numbers. Sometimes in the interest of a uniform notation for functions, we write Sx instead of x′.

Next we have two axioms for μ (the smallest number such that) as follows.

A third axiom for μ must wait until we have defined ≤.

Now we introduce the central feature of the system, the following rule of definition.

RD. Let Φ be a previously unused symbol. Then we can introduce it by a pair of definitions of the following form (n ≥ 0),

where F(x1, …, xn) is a wff in which no symbol occurs which was not previously defined (in particular, not Φ), and in which no free variables occur other than x1, …, xn (and possibly not all of these), and G(x1, …, xn, y) is a wff in which no free variables occur other than x1, …, xn, y (and possibly not all of these), and in which no symbol occurs which was not previously defined, except that Φ may occur but only if its last argument is y.