No CrossRef data available.
Article contents
A problem in recursive function theory
Published online by Cambridge University Press: 12 March 2014
Extract
In a recent paper [4] on mean value theorems in recursive function theory we proved the theorem that
(A) iff(n, x) is relatively differentiable with a relative derivative f1(n, x), for a ≤ x ≤ b, and if f(n, a) = f(n, b) = 0 relative to n,
then there is a recursive function ck, a < ck < b, and a recursive R(k) such that f1(n, ck) = 0(k) for n ≥ R(k); and we showed further that the added condition
(B) f(n, x) is either relatively variable or relatively constant
suffices to ensure that ck is uniformly contained in (a, b), i.e. that there exist α, β such that
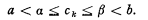
A comparison with the conditions under which Rolle's theorem is established in classical analysis suggests that clause (A) itself might suffice to ensure that ck is uniformly contained in (a, b); for in the classical theory there is a single point c, a < c < b, for which lim f1(n, c) = 0, and therefore f1(n, c) = 0(k) for sufficiently great values of n, where of course c is independent of k.
The object of the present note is to show that this is not in fact the case, and we shall construct a recursive function f(n, x) satisfying condition (A) in the interval (0, 1) and such that any sequence ck for which f1(n, ck) = 0(k) for large enough values of n is not uniformly contained in (0, 1).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953


