Article contents
Quantification theory and empty individual-domains
Published online by Cambridge University Press: 12 March 2014
Extract
In a recent paper by Mostowski [1] we find an investigation of those formulas of quantification theory which are valid in all domains of individuals, including the empty domain. Mostowski gives a complete set of axioms for such a first order functional calculus (the system is called “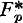 ”) and a comparison is made with a form of the usual calculus, Church's
”) and a comparison is made with a form of the usual calculus, Church's 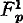 in [2]. It is pointed out that
in [2]. It is pointed out that 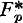 is much less elegant; in particular, the distributivity laws for quantifiers (e.g., (x){A . B)
is much less elegant; in particular, the distributivity laws for quantifiers (e.g., (x){A . B) 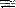 .{x)A . (x)B) do not hold in general, and likewise the rule of modus ponens does not preserve validity in all cases.
.{x)A . (x)B) do not hold in general, and likewise the rule of modus ponens does not preserve validity in all cases.
In this paper we show that a not inelegant system is obtained if one modifies Mostowski's approach in two respects; and once this is done a somewhat neater proof of completeness can be given.
The first respect in which we diverge from Mostowski is in the treatment of vacuous quantifiers. For him if p has no free x, then (x)p and (∃x)p are both to have the same value (interpretation) as p1. But this is not the only way to assign values to vacuous quantifications. For when universal quantification is viewed as a generalized conjunction, the formula (x)Fx has the significance of Fa . Fb…. for as many conjunctands as there are individuals in the domain, and if Fx should have the “constant” value p, then (x)p is to mean the conjunction of p with itself for as many times as there are individuals in the domain (compare the arithmetical 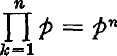 ).
).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1953
References
BIBLIOGRAPHY
- 18
- Cited by


