In this paper we discuss subsystems of number theory based on restrictions on induction in terms of quantifiers, and we show that all the natural formulations of ‘n-quantifier induction’ are reducible to one of two (for n ≠ 0) nonequivalent normal forms: the axiom of induction restricted to 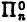 (or, equivalently,
(or, equivalently, 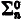 ) formulae and the rule of induction restricted to
) formulae and the rule of induction restricted to 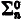 formulae.
formulae.
Let Z0 be classical elementary number theory with a symbol and defining equations for each Kalmar elementary function, and the rule of induction

restricted to quantifier-free formulae. Given the schema
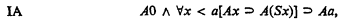
let IAn be the restriction of IA to formulae of Z0 with ≤n nested quantifiers, IAn′ to formulae with ≤n nested quantifiers, disregarding bounded quantifiers, 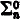 the restriction to
the restriction to 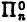 formulae,
formulae, 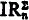 the restriction to
the restriction to 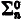 , formulae. IRn, IRn′,
, formulae. IRn, IRn′, 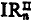 ,
, 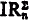 are analogous.
are analogous.
Then, we show that, for every n, 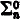 ,
, 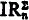 , IAn, and IAn′, are all equivalent modulo Z0. The corresponding statement does not hold for IR. We show that, if n ≠ 0,
, IAn, and IAn′, are all equivalent modulo Z0. The corresponding statement does not hold for IR. We show that, if n ≠ 0, 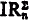 is reducible to
is reducible to 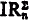 ; evidently IRn is reducible to
; evidently IRn is reducible to 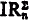 . On the other hand, IRn′ is obviously equivalent to IAn′ [10, Lemma 2].
. On the other hand, IRn′ is obviously equivalent to IAn′ [10, Lemma 2].
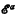 -arithmetic and transfinite induction
-arithmetic and transfinite induction