Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2025-01-05T14:50:21.701Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost strongly minimal theories. II

Published online by Cambridge University Press:  12 March 2014

John T. Baldwin
John T. Baldwin*
Affiliation:
Michigan State University, East Lansing, Michigan 48823
Get access Rights & Permissions [Opens in a new window]

Extract

The notion of an almost strongly minimal theory was introduced in [1]. Such a theory is a particularly simple sort of ℵ1-categorical theory. In [1] we characterized this simplicity in terms of the Stone space of models of T. Here, we characterize almost strongly minimal theories which are not ℵ0-categorical in terms of D. M. R. Park's notion [4] of a theory with the strong elementary intersection property. In addition we prove a useful sufficient condition for an elementary theory to be an almost strongly minimal theory. Our notation is from [1] but this paper is independent of the results proved there. We do assume familiarity with §1 and §2 of [2].

In [4], Park defines a theory T to have the strong elementary intersection property (s.e.i.p.) if for each model C of T and each pair 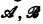of elementary submodels of C either 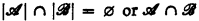is an elementary submodel of C. T has the nontrivial strong elementary intersection property (n.s.e.i.p.) if for each triple C, 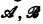as above 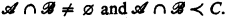Park proves the following two statements equivalent:

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 4 , December 1972 , pp. 657 - 660
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J. T., Almost strongly minimal theories. I, this Journal, vol. 37 (1972), pp. 487–493.Google Scholar
[2]Baldwin, J. T. and Lachlan, A. H., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 79–96.Google Scholar
[3]Makowsky, J. A., A note on almost strongly minimal theories, Notices of the American Mathematical Society, vol. 19 (1972), p. A–333. Abstract 72T–E23.Google Scholar
[4]Park, D. M. R., Set theoretic constructions in model theory, Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, Mass., 1964.Google Scholar