In [1] the notions of strongly minimal formula and algebraic closure were applied to the study of ℵ1-categorical theories. In this paper we study a particularly simple class of ℵ1-categorical theories. We characterize this class in terms of the analysis of the Stone space of models of T given by Morley [3].

We assume familiarity with [1] and [3], but for convenience we list the principal results and definitions from those papers which are used here. Our notation is the same as in [1] with the following exceptions.

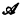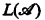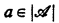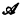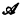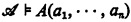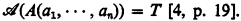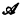We deal with a countable first order language L. We may extend the language L in several ways. If is an L-structure, there is a natural extension of L obtained by adjoining to L a constant a for each (the universe of ). For each sentence A(a1, …, an) ∈ L(A) we say satisfies A(a1, …, an) and write if in Shoenfield's notation If is an L-structure and X is a subset of 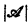, then L(X) is the language obtained by adjoining to L a name x for each 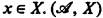is the natural expansion of 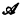to an L(X)-structure. A structure 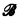is an inessential expansion [4, p. 141] of an L-structure 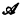if 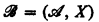for some .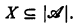