Research Article
On partitions of the real line into compact sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 353-359
-
- Article
- Export citation
Semiproper forcing axiom implies Martin maximum but not PFA+
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 360-367
-
- Article
- Export citation
A note on elementary equivalence of C(K) spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 368-373
-
- Article
- Export citation
Term models for weak set theories with a universal set
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 374-387
-
- Article
- Export citation
A hierarchy of filters on regular uncountable cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 388-395
-
- Article
- Export citation
Martin's axiom and a regular topological space with uncountable net weight whose countable product is hereditarily separable and hereditarily Lindelöf
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 396-399
-
- Article
- Export citation
Pas d'imaginaires dans l'infini!
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 400-403
-
- Article
- Export citation
Reduced coproducts of compact Hausdorff spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 404-424
-
- Article
- Export citation
On the consistency of self-referential systems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 425-436
-
- Article
- Export citation
Limit ultrapowers and abstract logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 437-454
-
- Article
- Export citation
A theory of properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 455-472
-
- Article
- Export citation
Systematization of finite many-valued logics through the method of tableaux
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 473-493
-
- Article
- Export citation
Provability in finite subtheories of PA and relative interpretability: a modal investigation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 494-511
-
- Article
- Export citation
Inconsistent nonstandard arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 512-518
-
- Article
- Export citation
Compact numeral representation with combinators
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 519-525
-
- Article
- Export citation
A contractionless semilattice semantics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 526-529
-
- Article
- Export citation
Complete Boolean ultraproducts
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 530-542
-
- Article
- Export citation
Isolated types in a weakly minimal set
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 543-547
-
- Article
- Export citation
On nontrivial types of U-rank 1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 548-551
-
- Article
- Export citation
Reviews
Paul Benacerraf. Mathematical truth. The journal of philosophy, vol. 70 (1973), pp. 661–679. - Michael Jubien. Ontology and mathematical truth. Noûs, vol. 11 (1977), pp. 133–150. - Philip Kitcher. The plight of the Platonist. Noûs, vol. 12 (1978), pp. 119–136.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 552-554
-
- Article
- Export citation

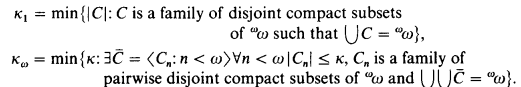
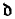 denote the least cardinality of a family
denote the least cardinality of a family 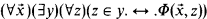
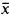
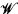 whose predicates refer to objects which are themselves predicates of the language—this particular interpretation being considered as the intended one.
whose predicates refer to objects which are themselves predicates of the language—this particular interpretation being considered as the intended one.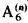 holds, and, besides, these models possess
holds, and, besides, these models possess 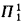 -indescribable cardinals. These two results imply the relative consistency of
-indescribable cardinals. These two results imply the relative consistency of 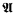 and
and 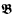 are countable models of a countable superstable theory without the finite cover property, then
are countable models of a countable superstable theory without the finite cover property, then 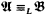 .
.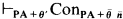 for every
for every