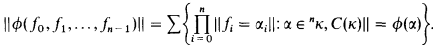Throughout this paper, B will always be a Boolean algebra and Γ an ultrafilter on B. We use + and Σ for the Boolean join operation and · and Π for the Boolean meet.

κ is always a regular cardinal. C(κ) is the full structure of κ, the structure with universe κ and whose functions and relations consist of all unitary functions and relations on κ. κB is the collection of all B-valued names for elements of κ. We use symbols f, g, h for members of κB. Formally an element f ∈ κB is a mapping κ → B with the properties that Σα∈κf(α) = 1B and that f(α) · f(β) = 0B whenever α ≠ β. We view f(α) as the Boolean-truth value indicating the extent to which the name f is equal to α, and we will hereafter write ∥f = α∥ for f(α). For every α ∈ κ there is a canonical name fα ∈ κB which has the property that ∥fα = α∥ = 1. Hereafter we identify α and fα.

If B is a κ+-complete Boolean algebra and Γ is an ultrafilter on B, then we may define the Boolean ultraproduct C(κ)B/Γ in the following manner. If ϕ(x0, x1, …, xn) is a formula of Lκ, the language for C(κ) (which has symbols for all finitary functions and relations on κ), and f0, f1, …, fn−1 are elements of κB then we define the Boolean-truth value of ϕ(f0, f1, …, fn−1) as