Tag systems were defined by Post [9], [10] and have been studied by a number of researchers including Minsky [7], Maslov [6] and Aanderaa and Belsnes [1]. In their recent paper Aanderaa and Belsnes demonstrated that every r.e. many-one degree (exclusive of the degree of the empty set) is represented by the general halting problem for tag systems, that is, by the family of halting problems ranging over all tag systems. Their result depends upon an informal proof of this property for Turing machines but may be seen to be correct in light of a formal proof due to Overbeek [8]. Our aim is to extend their results to the general word problem for these systems. Specifically, we shall present an effective method which, when applied to an arbitrary r.e. set S, where S is neither empty nor the set of all natural numbers, produces a tag system R′ whose word and halting problems are both of the same many-one degree as the decision problem for S. The proof is realized by first constructing, from the description of an arbitrary Turing machine M, which machine has at least one mortal and one immortal configuration, a 5-register machine R, whose word and halting problems are both of the same many-one degree as the halting problem for M. From R we then construct the desired tag system R′. This construction combined with Overbeek's [8] shows that every r.e. many-one degree (exclusive of the degrees of the empty set and the set of all natural numbers) is represented by the general word and halting problems for tag systems. Moreover our results are seen to be best possible with regard to degrees of unsolvability in that it is not the case that every nonrecursive r.e. one-one degree is represented by either of the general decision problems for tag systems which are considered here. These results were first shown in the author's thesis [3] and were announced in [4], They form part of an extensive study into the many-one equivalence of general decision problems. An overview of the initial findings of this research project may be found in [5].

This paper investigates the problem of extending the recursion theoretic construction of a minimal degree to the Kripke [2]-Platek [5] recursion theory on the ordinals less than an admissible ordinal α, a theory derived from the Takeuti [11] notion of a recursive function on the ordinal numbers. As noted in Sacks [7] when one generalizes the recursion theoretic definition of relative recursiveness to α-recursion theory for α > ω the two usual definitions give rise to two different notions of reducibility. We will show that whenever α is either a countable admissible or a regular cardinal of the constructible universe there is a subset of α whose degree is minimal for both notions of reducibility. The result is an excellent example of a theorem of ordinary recursion theory obtainable via two different constructions, one of which generalizes, the other of which does not. The construction which cannot be lifted to α-recursion theory is that of Spector [10]. We sketch the reasons for this in §3.

That elementary number theory is consistent and can be given a metamathematical consistency proof has been well known since Gentzen's 1936 paper, and a number of different proofs of this result have since been offered. What is presented here is essentially a simplified and generalized version of the proof given by Ackermann in 1940 [1]; but the proof given here applies to systems formalized in standard quantification theory rather than in Hilbert's ε-calculus, and is based upon the analysis of quantificational reasoning given by Herbrand's Fundamental Theorem. Dreben and Denton sketch such a proof in [2], but at a crucial point they follow Ackermann in tying the strategy of their proof too closely to the standard model. This makes the proof more complex than it need be and restricts its application to systems with induction on the standard well-ordering. The present proof is both simpler and more general in that it applies to systems ZR of number theory with induction on arbitrary recursive well-orderings R. This generalization was first obtained by Tait in [11] using functionals of lowest type. Some technical devices employed below are similar to ones used by Tait, but while the proof-theoretic methods employed here are naturally characterizable in terms of functionals of lowest type the present proof avoids the introduction of such functionals into the languages studied.

In this paper we develop certain methods of proof in Quine's set theory NF which have no counterparts elsewhere. These ideas were first used by Specker [5] in his disproof of the Axiom of Choice in NF. They depend on the properties of two related operations, T(n) on cardinal numbers and U(α) on ordinal numbers, which are defined by the equations

for each set x and well ordering R. (Here and below we use Rosser's notation [3].) The definitions insure that the formulas T(x) = y and U(x) = y are stratified when y is assigned a type one higher than x. The importance of T and U stems from the following facts: (i) each of T and U is a 1-1, order preserving operation from its domain onto a proper initial section of its domain; (ii) Tand U commute with most of the standard operations on cardinal and ordinal numbers.

These basic facts are discussed in §1. In §2 we prove in NF that the exponential function 2n is not 1-1. Indeed, there exist cardinal numbers m and n which satisfy

In §3 we prove the following technical result, which has many important applications. Suppose f is an increasing function from an initial segment S of the set NO of ordinal numbers into NO and that f commutes with U.

Permutation methods for proving relative consistency results were first applied to Quine's set theory NF by Dana Scott [5]. He showed that the sentence (∃x)(x = {x}), which asserts the existence of individuals in Quine's sense, and its negation are each consistent relative to NF. In this paper Scott's method is shown to apply to any extension T of NF whose axioms are invariant in a certain sense. (Every stratified sentence is invariant, as are many interesting unstratified sentences, such as Rosser's Counting Axiom and the sentence which asserts that every Cantorian set is strongly Cantorian.) We also use this method to prove a number of interesting relative consistency results for such extensions T of NF.

Our main result (Theorem 2.4) asserts that it is consistent relative to T to assume that every well ordering of a strongly Cantorian set is order isomorphic to the well ordering by ∈ of a von Neumann ordinal. (The restriction to strongly Cantorian sets is necessary.) Therefore, although one cannot develop within NF a satisfactory theory of von Neumann ordinals, due to the many unstratified formulas which arise, our result shows that one can consistently assume as rich a theory as is allowed by the extent to which T provides for strongly Cantorian sets. This seems to be the first such “positive” consistency result for NF, and we think that the permutation method will yield others.

The abstraction principle is

for K any formula not involving x. This is well known to be inconsistent and in [1] Hintikka proposed two modified versions of (0) which we briefly describe. First, he suggested

where K is any formula not involving x, and K+ is obtained from K by replacing subformulae of the form ∃zL by ∃z(z ≠ x ∧ L) and those of the form ∀zL by ∀z(z ≠ x → L), etc. The second version is

where K+ is a formula of the type described for (1) and z1 …, zk are all the free variables in (2).

The Arithmetical Hierarchy Theorem of Kleene [1] states that in the complete theory of the standard model of arithmetic there is for each positive integer r a Σr0 formula which is not equivalent to any Πr0 formula, and a Πr0 formula which is not equivalent to any Πr0 formula. A Πr0 formula is a formula of the form

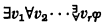
where φ has only bounded quantifiers; Πr0 formulas are defined dually.

The Linear Prefix Theorem in [3] is an analogous result for predicate logic. Consider the first order predicate logic L with identity symbol, countably many n-placed relation symbols for each n, and no constant or function symbols. A prefix is a finite sequence

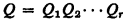
of quantifier symbols ∃ and ∀, for example ∀∃∀∀∀∃. By a Q formula we mean a formula of L of the form

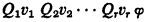
where v1, …, vr are distinct variables and φ has no quantifiers. A sentence is a formula with no free variables. The Linear Prefix Theorem is as follows.

Linear Prefix Theorem. Let Q and q be two different prefixes of the same length r. Then there is a Q sentence which is not logically equivalent to any q sentence.

Moreover, for each s there is a Q formula with s free variables which is not logically equivalent to any q formula with s free variables.

For example, there is an ∀∃∀∀∀∃ sentence which is not logically equivalent to any ∀∃∃∀∀∃ sentence, and vice versa. Recall that in arithmetic two consecutive ∃'s or ∀'s can be collapsed; for instance all ∀∃∀∀∀∃ and ∀∃∃∀∀∃ formulas are logically equivalent to Π40 formulas. But the Linear Prefix Theorem shows that in predicate logic the number of quantifiers in each block, as well as the number of blocks, counts.

Let T be a set of axioms for a classical theory TC (e.g. abelian groups, linear order, unary function, algebraically closed fields, etc.). Suppose we regard T as a set of axioms for an intuitionistic theory TH (more precisely, we regard T as axioms in Heyting's predicate calculus HPC).

Question. Is TH decidable (or, more generally, if X is any intermediate logic, is TX decidable)? In [1] we gave sufficient conditions for the undecidability of TH. These conditions depend on the formulas of T (different axiomatization of the same TC may give rise to different TH) and on the classical model theoretic properties of TC (the method did not work for model complete theories, e.g. those of the title of the paper). For details see [1]. In [2] we gave some decidability results for some theories: The problem of the decidability of theories TH for a classically model complete TC remained open. An undecidability result in this direction, for dense linear order was obtained by Smorynski [4]. The cases of algebraically closed fields and real closed fields and divisible abelian groups are treated in this paper. Other various decidability results of the intuitionistic theories were obtained by several authors, see [1], [2], [4] for details.

One more remark before we start. There are several possible formulations for an intuitionistic theory of, e.g. fields, that correspond to several possible axiomatizations of the classical theory. Other formulations may be given in terms of the apartness relation, such as the one for fields given by Heyting [5]. The formulations that we consider here are of interest as these systems occur in intuitionistic mathematics. We hope that the present methods could be extended to the (more interesting) case of Heyting's systems [5].

This paper is a survey and a synthesis of the various approaches to defining algebraic elements. Most of it is devoted to proving the following result.

Let T be a universal theory with the Amalgamation Property. Then for T the notions of algebraic element introduced by Robinson, Jónsson, and Morley are identical. Furthermore, they extend in a natural way the notion of algebraic element introduced by Park, and used by Lachlan and Baldwin and by Kueker.

In the course of proving this we shall construct the algebraic closure as a suitable injective hull and prove a unique factorisation theorem for algebraic predicates.

We shall also show (in §3) that if T is closed under products then algebraic elements all have degree 1. Thus in algebra, algebraic elements reduce to epimorphisms.

To demonstrate the remarkable stability of the notion we shall show (at the end of §5) that defining algebraic elements by infinitary formulas yields no new ones.

Let L be a language. The cardinality of the set of formulas of L is denoted by ∣L∣. An L-theory is a deductively closed set of L-sentences. We let denote the category of models of T and (L-structure) homomorphisms between them. If A is a substructure of B we write A ≤ B. We call u: A → B an injection if u is an isomorphism of A with a substructure of B, and let denote the subcategory of consisting of all injections.

The present paper concerns itself primarily with the decision problem for formal elementary intuitionistic theories and the method is primarily model-theoretic. The chief tool is the Kripke model for which the reader may find sufficient background in Fitting's book Intuitionistic logic model theory and forcing (North-Holland, Amsterdam, 1969). Our notation is basically that of Fitting, the differences being to favor more standard notations in various places.

The author owes a great debt to many people and would particularly like to thank S. Feferman, D. Gabbay, W. Howard, G. Kreisel, G. Mints, and R. Statman for their valuable assistance.

The method of elimination of quantifiers, which has long since proven its use in classical logic, has also been applied to intuitionistic theories (i) to demonstrate decidability ([9], [15], [17]), (ii) to prove the coincidence of an intuitionistic theory with its classical extension ([9], [17]), and (iii), as we will see below, to establish relations between an intuitionistic theory and its classical extension. The most general of these results is to be obtained from the method of Lifshits' quantifier elimination for the intuitionistic theory of decidable equality.

Since the details of Lifshits' proof have not been published, and since the proof yields a more general result than that stated in his abstract [15], we include the proof and several corollaries.