Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T20:51:59.004Z Has data issue: false hasContentIssue false
  • English
  • Français

Defining algebraic elements

Published online by Cambridge University Press:  12 March 2014

Paul D. Bacsich
Paul D. Bacsich*
Affiliation:
University of Oxford, Mathematical Institute, Oxford, England
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is a survey and a synthesis of the various approaches to defining algebraic elements. Most of it is devoted to proving the following result.

Let T be a universal theory with the Amalgamation Property. Then for T the notions of algebraic element introduced by Robinson, Jónsson, and Morley are identical. Furthermore, they extend in a natural way the notion of algebraic element introduced by Park, and used by Lachlan and Baldwin and by Kueker.

In the course of proving this we shall construct the algebraic closure as a suitable injective hull and prove a unique factorisation theorem for algebraic predicates.

We shall also show (in §3) that if T is closed under products then algebraic elements all have degree 1. Thus in algebra, algebraic elements reduce to epimorphisms.

To demonstrate the remarkable stability of the notion we shall show (at the end of §5) that defining algebraic elements by infinitary formulas yields no new ones.

Let L be a language. The cardinality of the set of formulas of L is denoted by ∣L∣. An L-theory is a deductively closed set of L-sentences. We let 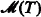denote the category of models of T and (L-structure) homomorphisms between them. If A is a substructure of B we write A ≤ B. We call u: A → B an injection if u is an isomorphism of A with a substructure of B, and let 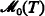denote the subcategory of 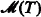consisting of all injections.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 38 , Issue 1 , March 1973 , pp. 93 - 101
Copyright
Copyright © Association for Symbolic Logic 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bacsich, P., An epi-reflector for universal theories, Canadian Mathematical Bulletin (to appear).Google Scholar
[2]Bacsich, P., Model theory of epimorphisms, Canadian Mathematical Bulletin (to appear).Google Scholar
[3]Baldwin, J. and Lachlan, A., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 79–96.Google Scholar
[4]Banaschewski, B., Injectivity and essential extensions in equational classes of algebras, Proceedings of the Conference on Universal Algebra, Queen's papers, no. 25.Google Scholar
[S]Eklof, P. and Sabbagh, G., Model-completions and modules, Annals of Mathematical Logic, vol. 3 (1971), pp. 251–295.CrossRefGoogle Scholar
[6]Grätzer, G., Universal algebra, Van Nostrand, Princeton, N.J., 1968.Google Scholar
[7]Jónsson, B., Algebraic extensions of relational systems, Mathematica Scandinavica, vol. 11 (1962), pp. 179–205.CrossRefGoogle Scholar
[8]Jónsson, B., Extensions of relational structures, The theory of models, North-Holland, Amsterdam, 1965.Google Scholar
[9]Kueker, D., Generalised interpolation and definability, Annals of Mathematical Logic, vol. 1 (1970), pp. 423–468.CrossRefGoogle Scholar
[10]Morley, M., Categoricity in power, Transactions of the American Mathematical Society, vol. 114 (1965), pp. 514–538.CrossRefGoogle Scholar
[11]Park, D., Set theoretic constructions in model theory, Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, Mass., 1964.Google Scholar
[12]Robinson, A., On the metamathematics of algebra, North-Holland, Amsterdam, 1951.Google Scholar
[13]Robinson, A., Introduction to model theory and the metamathematics of algebra, North-Holland, Amsterdam, 1965.Google Scholar
[14]Robinson, A., On the notion of algebraic closedness for noncommutative groups and fields, this Journal, vol. 36 (1971), pp. 441–444.Google Scholar
[15]Sacks, G., Saturated model theory, Benjamin, New York, 1972.Google Scholar