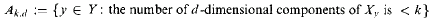Research Article
Arithmetical independence results using higher recursion theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-8
-
- Article
- Export citation
Construction of saturated quasi-minimal structure
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 9-22
-
- Article
- Export citation
Sous-groupes de Carter dans les groupes de rang de Morley fini
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 23-33
-
- Article
- Export citation
Some remarks on one-basedness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 34-38
-
- Article
- Export citation
P versus NP and computability theoretic constructions in complexity theory over algebraic structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 39-64
-
- Article
- Export citation
Hindman's theorem, ultrafilters, and reverse mathematics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 65-72
-
- Article
- Export citation
Generic Σ31 absoluteness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 73-80
-
- Article
- Export citation
Two step iteration of almost disjoint families
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 81-90
-
- Article
- Export citation
Valuation theoretic content of the Marker-Steinhorn theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 91-93
-
- Article
- Export citation
A weak variation of shelah's I[ω2]
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 94-100
-
- Article
- Export citation
Analytic countably splitting families
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 101-117
-
- Article
- Export citation
First order quantifiers in monadic second order logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 118-136
-
- Article
- Export citation
Model theory of comodules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 137-142
-
- Article
- Export citation
Splittings of effectively speedable sets and effectively levelable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 143-158
-
- Article
- Export citation
A definable nonstandard model of the reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 159-164
-
- Article
- Export citation
Standard sets in nonstandard set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 165-182
-
- Article
- Export citation
Truth definitions in finite models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 183-200
-
- Article
- Export citation
Approximate Euler characteristic, dimension, and weak pigeonhole principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 201-214
-
- Article
- Export citation
Forking and independence in o-minimal theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 215-240
-
- Article
- Export citation
A definability result for compact complex spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 241-254
-
- Article
- Export citation

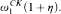 . These sentences allow us to build completions {
. These sentences allow us to build completions {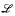 the class of
the class of 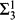 absoluteness (with real parameters) in various types of generic extensions, correcting and improving some results from [3]. (In particular, see Theorem 3 below.) We shall also make some comments relating this work to the bounded forcing axioms BMM, BPFA and BSPFA.
absoluteness (with real parameters) in various types of generic extensions, correcting and improving some results from [3]. (In particular, see Theorem 3 below.) We shall also make some comments relating this work to the bounded forcing axioms BMM, BPFA and BSPFA. ⊂ [
⊂ [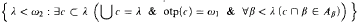
 (
( does not depend on the syntax of
does not depend on the syntax of 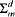 classes (prenex classes of higher order logics) define FM-truth. For any
classes (prenex classes of higher order logics) define FM-truth. For any 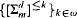 of syntactically defined fragments of
of syntactically defined fragments of 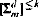 classes to give a refinement of known results on the complexity classes captured by
classes to give a refinement of known results on the complexity classes captured by 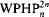 : two disjoint copies of a non-empty definable set
: two disjoint copies of a non-empty definable set  : for no definable set
: for no definable set