Research Article
Canonical functions, non-regular ultrafilters and Ulam's problem on ω1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 713-739
-
- Article
- Export citation
Generality of proofs and its Brauerian representation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 740-750
-
- Article
- Export citation
The completeness of Heyting first-order logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 751-763
-
- Article
- Export citation
Ultrafilters on the natural numbers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 764-784
-
- Article
- Export citation
Transfer methods for o-minimal topology
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 785-794
-
- Article
- Export citation
A proof–technique in uniform space theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 795-802
-
- Article
- Export citation
Expansions of geometries
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 803-827
-
- Article
- Export citation
Positive abstraction and extensionality
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 828-836
-
- Article
- Export citation
Fat sets and saturated ideals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 837-845
-
- Article
- Export citation
Discouraging results for ultraimaginary independence theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 846-850
-
- Article
- Export citation
Strong normalization proof with CPS-translation for second order classical natural deduction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 851-859
-
- Article
- Export citation
Existential definability with bounds on archimedean valuations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 860-878
-
- Article
- Export citation
Non-well-foundedness of well-orderable power sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 879-884
-
- Article
- Export citation
The approximation structure of a computably approximable real
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 885-922
-
- Article
- Export citation
Differential forms in the model theory of differential fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 923-945
-
- Article
- Export citation
Elementary properties of the Boolean hull and reduced quotient functors
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 946-971
-
- Article
- Export citation
A hierarchy for the plus cupping Turing degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 972-988
-
- Article
- Export citation
Embedding jump upper semilattices into the Turing degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 989-1014
-
- Article
- Export citation
Classical and constructive hierarchies in extended intuitionistic analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1015-1043
-
- Article
- Export citation
Isomorphisms of splits of computably enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1044-1064
-
- Article
- Export citation

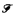 of
of 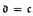 . This result, taken along with our result that there exists a
. This result, taken along with our result that there exists a 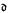 .
.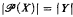 .
.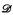 , where a jump upper semilattice (jusl) is an upper semilattice endowed with a strictly increasing and monotone unary operator that we call jump, and
, where a jump upper semilattice (jusl) is an upper semilattice endowed with a strictly increasing and monotone unary operator that we call jump, and 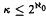 is embeddable in
is embeddable in 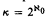 the answer is no, and that for
the answer is no, and that for 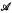 of Kleene's axiomatization of Brouwer's intuitionistic analysis, in which the classical arithmetical and analytical hierarchies are faithfully represented as hierarchies of the domains of continuity. A
of Kleene's axiomatization of Brouwer's intuitionistic analysis, in which the classical arithmetical and analytical hierarchies are faithfully represented as hierarchies of the domains of continuity. A  are automorphic via Φ then the structures
are automorphic via Φ then the structures  (
(