Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-02T04:41:43.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Classical and constructive hierarchies in extended intuitionistic analysis

Published online by Cambridge University Press:  12 March 2014

Joan Rand Moschovakis
Joan Rand Moschovakis*
Affiliation:
Graduate Program in Logic and Algorithms (MPLA), Department of Mathematics, University of Athens, Athens, Greece
*
721 24th Street, Santa Monica, CA 90402, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper introduces an extension 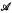of Kleene's axiomatization of Brouwer's intuitionistic analysis, in which the classical arithmetical and analytical hierarchies are faithfully represented as hierarchies of the domains of continuity. A domain of continuity is a relation R(α) on Baire space with the property that every constructive partial functional defined on {α: R(α)} is continuous there. The domains of continuity for 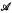coincide with the stable relations (those equivalent in 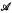to their double negations), while every relation R(α) is equivalent in 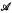to ∃βA(α, β) for some stable A(α, β) (which belongs to the classical analytical hierarchy).

The logic of 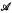is intuitionistic. The axioms of 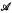include countable comprehension, bar induction, Troelstra's generalized continuous choice, primitive recursive Markov's Principle and a classical axiom of dependent choices proposed by Krauss. Constructive dependent choices, and constructive and classical countable choice, are theorems, 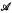is maximal with respect to classical Kleene function realizability, which establishes its consistency. The usual disjunction and (recursive) existence properties ensure that 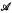preserves the constructive sense of “or” and “there exists.”

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 68 , Issue 3 , September 2003 , pp. 1015 - 1043
Copyright
Copyright © Association for Symbolic Logic 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Beeson, M. J., Problematic principles in constructive mathematics, Logic colloquium '80 (Lascar, D. van Dalen, D. and Smiley, T. J., editors), North-Holland, Amsterdam, 1982.Google Scholar
[2] Beeson, M. J., Foundations of Constructive Mathematics, Springer, Berlin, 1985.CrossRefGoogle Scholar
[3] Bishop, E., Foundations of Constructive Analysis, McGraw-Hill, New York, 1967.Google Scholar
[4] Diaconescu, R., Axiom of choice and complementation, Proceedings of the American Mathematical Society, vol. 51 (1975), pp. 176–178.CrossRefGoogle Scholar
[5] Gödel, K., On intuitionistic arithmetic and number theory, Kurt Gödel: Collected Works, Volume I (Feferman, S. et al., editors), Oxford University Press, New York, 1993, translated by Bauer-Mengelberg, S. and van Heijenoort, J., pp. 287–295.Google Scholar
[6] Kleene, S. C., Introduction to Metamathematics, North-Holland, Amsterdam, 1952.Google Scholar
[7] Kleene, S. C., Realizability and Shanin's algorithm for the constructive deciphering of mathematical sentences, Logique et Analyse, Nouvelle Série, vol. 3 (1960), pp. 154–165.Google Scholar
[8] Kleene, S. C., Classical extensions of intuitionistic mathematics, Logic, methodology and philosophy of science, proceedings of the 1964 international congress (Amsterdam) (Bar-Hillel, Y., editor), North-Holland, 1965, pp. 31–44.Google Scholar
[9] Kleene, S. C., Formalized recursive functionals and formalized realizability, Memoirs, no. 89, American Mathematical Society, 1969.CrossRefGoogle Scholar
[10] Kleene, S. C. and Vesley, R. E., The Foundations of Intuitionistic Mathematics, Especially in Relation to Recursive Functions, North-Holland, Amsterdam, 1965.Google Scholar
[11] Krauss, P. H., A constructive interpretation of classical mathematics, Mathematische Schriften Kassel, preprint No. 5/92, 1992.Google Scholar
[12] Moschovakis, J. R., Disjunction, existence and λ-elimination, Ph.D. thesis , University of Wisconsin, 1965.Google Scholar
[13] Moschovakis, J. R., Can there be no non-recursive functions, this Journal, vol. 36 (1971), pp. 309–315.Google Scholar
[14] Moschovakis, J. R., Analyzing realizability by Troelstra's methods, Annals of Pure and Applied Logic, vol. 114 (2002), pp. 203–225.Google Scholar
[15] Moschovakis, Y. N., Descriptive Set Theory, North-Holland, Amsterdam, 1980.Google Scholar
[16] Troelstra, A. S. (editor), Metamathematical Investigation of Intuitionistic Arithmetic and Analysis, Lecture Notes in Mathematics, no. 344, Springer Verlag, Berlin, Heidelberg, New York, 1973, with contributions by Troelstra, A. S., Smorynski, C. A., Zucker, J. I. and Howard, W. A..CrossRefGoogle Scholar
[17] Troelstra, A. S., Intuitionistic extensions of the reals II, Logic Colloquium '80 (Amsterdam) (Lascar, D. van Dalen, D. and Smiley, T. J., editors), North-Holland, 1982, pp. 279–310.Google Scholar
[18] Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics: An Introduction, vol. 1 and 2, North-Holland, Amsterdam, 1988.Google Scholar
[19] Veldman, W., Investigations in intuitionistic hierarchy theory, Ph.D. thesis , Catholic University of Nijmegen, 1981.Google Scholar
[20] Veldman, W., A survey of intuitionistic descriptive set theory, Mathematical Logic, Proceedings of the Heyting Conference 1988 (New York and London) (Petkov, P. P., editor), Plenum Press, 1990, pp. 155–174.Google Scholar
[21] Veldman, W., The Borel hierarchy and the projective hierarchy in intuitionistic mathematics, University of Nijmegen Department of Mathematics Report No. 0103, 03 2001.Google Scholar
[22] Veldman, W., On some sets that are not positively Borel, University of Nijmegen Department of Mathematics Report No. 0201, 01 2002.Google Scholar
[23] Veldman, W., On the persistent difficulty of disjunction, Proceedings of the XIth International Congress on Logic, Methodology and Philosophy of Science, held in Cracow, Poland, 1999, forthcoming.Google Scholar