Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-31T19:27:48.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding jump upper semilattices into the Turing degrees

Published online by Cambridge University Press:  12 March 2014

Antonio Montalbán
Antonio Montalbán*
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that every countable jump upper semilattice can be embedded in 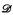, where a jump upper semilattice (jusl) is an upper semilattice endowed with a strictly increasing and monotone unary operator that we call jump, and 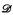is the jusl of Turing degrees. As a corollary we get that the existential theory of 〈D, ≤T, ∨, ′〉 is decidable. We also prove that this result is not true about jusls with 0, by proving that not every quantifier free 1-type of jusl with 0 is realized in 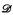. On the other hand, we show that every quantifier free 1-type of jump partial ordering (jpo) with 0 is realized in 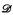. Moreover, we show that if every quantifier free type, p(x1,…, xn), of jpo with 0, which contains the formula x1 ≤ 0(m) & … & xn ≤ 0(m) for some m, is realized in 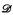, then every quantifier free type of jpo with 0 is realized in .

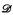We also study the question of whether every jusl with the c.p.p. and size 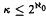is embeddable in 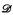. We show that for 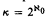the answer is no, and that for κ = ℵ1 it is independent of ZFC. (It is true if MA(κ) holds.)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 68 , Issue 3 , September 2003 , pp. 989 - 1014
Copyright
Copyright © Association for Symbolic Logic 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Abraham, U. and Shore, R.A., Initial segments of the degrees of size ℵ1 , Israel Journal of Mathematics, vol. 53 (1986), pp. 1–51.Google Scholar
[2] Ash, C.J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Elsevier Science, 2000.Google Scholar
[3] Downey, R.G., Computability theory and linear orderings, Handbook of Recursive Mathematics, vol. 2, North Holland, 1998, pp. 823–976.Google Scholar
[4] Harrison, J., Recursive pseudo-well-orderings, Transactions of the American Mathematical Society, vol. 131 (1968), pp. 526–543.Google Scholar
[5] Hinman, P.G., Jump traces with large gaps, Recursion theory and complexity (Arslanov, M. M. and Lempp, S., editors), 1999, pp. 71–80.Google Scholar
[6] Hinman, P.G. and Slaman, T.A., Jump embeddings in the Turing degrees, this Journal, vol. 56 (1991), pp. 563–591.Google Scholar
[7] Hodges, W., Model Theory, Cambridge Univeristy Press, Cambridge, 1993.Google Scholar
[8] Jech, T., Set Theory, third millennium ed., Springer, 2003.Google Scholar
[9] Jockusch, C.G. Jr and Slaman, T.A., On the Σ2 theory of the upper semilattice of the Turing degrees, this Journal, vol. 58 (1993), pp. 193–204.Google Scholar
[10] Kleene, S.C. and Post, E.L., The upper semi-lattice of the degrees of recursive unsolvability, Annals of Mathematics, vol. 59 (1954), pp. 379–407.Google Scholar
[11] Kunen, K., Set Theory, An Introduction to Independence Proofs, North Holland, Amsterdam, 1980.Google Scholar
[12] Lachlan, A.H., Distributive initial segments of the degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 457–472.Google Scholar
[13] Lempp, S. and Lerman, M., The decidability of the existential theory of the poset of the recursively enumerable degrees with jump relations, Advances in Mathematics, vol. 120 (1996), pp. 1–142.Google Scholar
[14] Lerman, M., Degrees of Unsolvability, Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1983.Google Scholar
[15] Sacks, G.E., On suborderings of degrees of recursive unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 7 (1961), pp. 46–56.Google Scholar
[16] Sacks, G.E., Higher Recursion Theory, Springer-Verlag, Berlin, Heidelberg, 1990.Google Scholar
[17] Shore, R.A. and Slaman, T.A., The ∀∃ theory of D(≤, ∨, ′) is undecidable, In preparation.Google Scholar
[18] Slaman, T.A. and Woodin, W.H., Definability in degree structures, Monograph in preparation.Google Scholar