In [MP] Marker and Pillay showed that if X ⊂ Cn is constructible but (C, +, X) is not locally modular, then multiplication is definable in the structure (C, +,X). That result extended earlier results of Martin [M] and Rabinovich and Zil'ber [RZ]. Here we will examine additive reducts of R and Qp.
Definition. A subset X of Rn is called semialgebraic if it is definable in the structure (R, +,·). A subset X of Rn is called semilinear if it is definable in the structure (R, +, <,λr)r∈b, where λr is the function x ↦ rx [scalar multiplication by r].
Every semilinear set is a Boolean combination of sets of the form {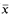 : p (
: p (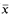 ) = 0} and {
) = 0} and {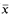 : q(
: q(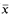 ) > 0}, where p(
) > 0}, where p(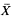 ) and q(
) and q(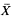 ) are linear polynomials.
) are linear polynomials.
Van den Dries asked the following question: if X is semialgebraic but not semilinear, can we define multiplication in (R, +, <,X)? This was answered negatively by Pillay, Scowcroft and Steinhorn.
Theorem 1.1 [PSS]. Suppose X ⊂ Rnis semialgebraic and X ⊂ Infor some bounded interval I. Then multiplication is not definable in (R, +, <,X,λr)r∈R.
In particular if X = · ∣ [0, l ]2, the graph of multiplication restricted to the unit interval, then X is not semilinear so we have a negative answer to van den Dries' question. Peterzil showed that this is the only restriction.