In [2], Juhasz and Shelah use a forcing argument to show that it is consistent with GCH that there is a 0-dimensional T2 topological space X of cardinality ℵ3 such that every partition of the triples of X into countably many pieces has a nondiscrete (in the topology) homogeneous set. In this paper we will show how to construct such a space using a simplified (ω2, 1)-morass with certain additional structure added to it. The additional structure will be a slight strengthening of a built-in ◊ sequence, analogous to the strengthening of ordinary ◊k to ◊S for a stationary set S ⊆ k.

Suppose 〈〈θα∣ ∝ ≤ ω2〉, 〈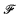∝β∣α < β ≤ ω2〉〉 is a neat simplified (ω2, 1)-morass (see [3]). Let ℒ be a language with countably many symbols of all types, and suppose that for each α < ω2, 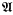α is an ℒ-structure with universe θα. The sequence 〈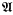α∣α < ω2 is called a built-in ◊ sequence for the morass if for every ℒ-structure 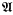with universe ω3 there is some α < ω2 and some f ∈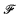αω2 such that f(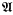α) ≺ 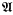, where f(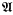α) is the ℒ-structure isomorphic to 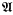α under the isomorphism f. We can strengthen this slightly by assuming that 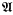α is only defined for α ∈ S, for some stationary set S ⊆ ω2. We will then say that 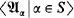is a built-in ◊ sequence on levels in S if for every ℒ-structure 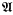with universe ω3 there is some α ∈ S and some f ∈ 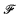αω2 such that f(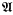α) ≺ 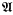.