Errata
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. iv
-
- Article
-
- You have access
- Export citation
Research Article
Postulates for the calculus of binary relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 85-97
-
- Article
- Export citation
Sur les types des propositions composées
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 98-103
-
- Article
- Export citation
Elimination of extra-logical postulates
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 104-109
-
- Article
- Export citation
Proof that there are infinitely many modalities in Lewis's system S2
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 110-112
-
- Article
- Export citation
Reviews
Henry S. Leonard and Nelson Goodman. The calculus of individuals and its uses. The journal of symbolic logic, vol. 5 (1940), pp. 45–55.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 113-114
-
- Article
- Export citation
Alonzo Church. A formulation of the simple theory of types. The journal of symbolic logic, vol. 5 (1940), pp. 56–68.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 114-115
-
- Article
- Export citation
Alfred Takski. On undecidable statements in enlarged systems of logic and the concept of truth. The journal of symbolic logic, vol. 4 (1939), pp. 105–112. - Andrzej Mostowski. Bemerkungen turn Begriff der inhaltlichen Widerspruchsfreiheit. The journal of symbolic logic, vol. 4 (1939), pp. 113–114.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 115-116
-
- Article
- Export citation
Kurt Gödel. The consistency of the axiom of choice and of the generalized continuum-hypothesis. Proceedings of the National Academy of Sciences, vol. 24 (1938), pp. 556–557.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 116-117
-
- Article
- Export citation
Kurt Gödel. Consistency-proof for the generalized continuum-hypothesis. Proceedings of the National Academy of Sciences, vol. 25 (1939), pp. 220–224.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 117-118
-
- Article
- Export citation
V. N. Molodšij. Zaméčaniá k stat′é L. P. Gokiéli “O ponálii funkcii” (Remarks on the article L. P. Gokiéli “O ponátii funkcii”). Trudy Tbilisskogo Matématičéskogo Instituta (Travaux de l'Institut Mathématique de Tbilissi), vol. 6 (1939), pp. 1–14. - L. P. Gokiéli. O matématiké “vozmožnosti” i matématiké “déjstvitél′nosti” (On the mathematics “of possibility” and the mathematics “of actuality”). Proceedings of the National Academy of Sciences, vol. 24 (1938), pp. 15–96.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 118-119
-
- Article
- Export citation
D. A. Bochvar. Über einen Aussagenkalkül mit abzählbaren logischen Summen und Produkten. Matématičéskij sbornik (Recueil mathématique), n. s. vol. 7 (1940), pp. 65–100.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 119
-
- Article
- Export citation
A. Errera. Sur les fondements de l'arithmétique. Comptes rendus du Congrès des Sciences Mathématiques de Liége (17–22 juillet 1939), Georges Thone, Liége, pp. 123–127.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 119-120
-
- Article
- Export citation
D. Mordoukhay-Boltovskoy. Sur les syllogismes en logique et les hypersyllogismes en métalogique. Bulletin de la Société Physico-mathématique de Kazan, ser. 3 vol. 10 (1938), pp. 161–172.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 120
-
- Article
- Export citation
E. Abita. Nuovi indirritzi della logica formale. Esercitazioni matematiche, vol. 12 (1940), pp. 88–99.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 120
-
- Article
- Export citation
Abraham Kaplan and Irving M. Copilowish. Must there be propositions?Mind, n. s. vol. 48 (1939), pp. 478–484.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 120
-
- Article
- Export citation
Max Black. Some problems connected with language. Proceedings of the Aristotelian Society, vol. 39 (1938–1939), pp. 43–68.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 120-121
-
- Article
- Export citation
M. Black. Comments on a recent version of phenomenalism. Analysis, vol. 7 no. 1 (121939), pp. 1–12.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 121
-
- Article
- Export citation
Norman Malcolm. Are necessary propositions really verbal?Mind, n. s. vol. 49 (1940), pp. 189–203.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 121-122
-
- Article
- Export citation
Maurice Fréchet. The diverse definitions of probability. The journal of unified science (Erkenntnis) vol. 8 (1939), pp. 7–23.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 122-123
-
- Article
- Export citation

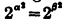 , then α=β. This theorem has not been proved, however, except on the assumption of the axiom of choice and the generalized continuum hypothesis, and is not assumed in the present paper.
, then α=β. This theorem has not been proved, however, except on the assumption of the axiom of choice and the generalized continuum hypothesis, and is not assumed in the present paper.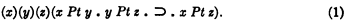
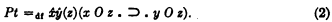
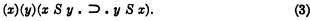
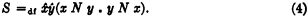
 , so that
, so that 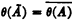 . For, if
. For, if