Published online by Cambridge University Press: 12 March 2014
The theory of relations was discussed, along with the theory of classes, by Peirce and Schröder. While the calculus of classes has subsequently been presented (by Couturat, and by Huntington) as an abstract mathematical system, no similar formulation has been published of the calculus of relations. Professor Alfred Tarski has proposed to me, the problem of developing a similar formulation for the theory of relations. In this paper I present a set of postulates for the calculus of relations.
The postulates have been chosen so as to enable us to prove Theorem A, below, which asserts a kind of completeness of the system. A set of postulates is called semi-categorical, if every two realizations which involve the same number of elements are isomorphic. From Theorem A one can easily prove that my postulates are semi-categorical, if one assumes the following theorem from Mengenlehre: if α and β are cardinal numbers such that 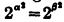 , then α=β. This theorem has not been proved, however, except on the assumption of the axiom of choice and the generalized continuum hypothesis, and is not assumed in the present paper.
, then α=β. This theorem has not been proved, however, except on the assumption of the axiom of choice and the generalized continuum hypothesis, and is not assumed in the present paper.
It should be pointed out, that the sort of completeness I have chosen is not the only sort, or even necessarily the most interesting sort, of completeness which a set of postulates for the calculus of relations could possess. For example, the question arises, whether it would be possible to find a set of postulates from which all true equations (involving free variables and the operations used by Schröder) could be derived, and which was the weakest possible such set. The present work should therefore be regarded only as a first step in the investigation of the axiomatization of the calculus of relations.
1 The notion of semi-categoricity is due to Tarski. See Zur Grundlegung der Booleschen Algebra I, Fundamenta mathematicae, vol. 24 (1935), pp. 177–198CrossRefGoogle Scholar.
I take this opportunity to express my gratitude to Professor Tarski for his many helpful suggestions in connection with the present paper.
2 Loc. cit. I shall assume, however, that a complete atomic Boolean algebra contains at least two elements.